
Question Number 205767 by lmcp1203 last updated on 30/Mar/24
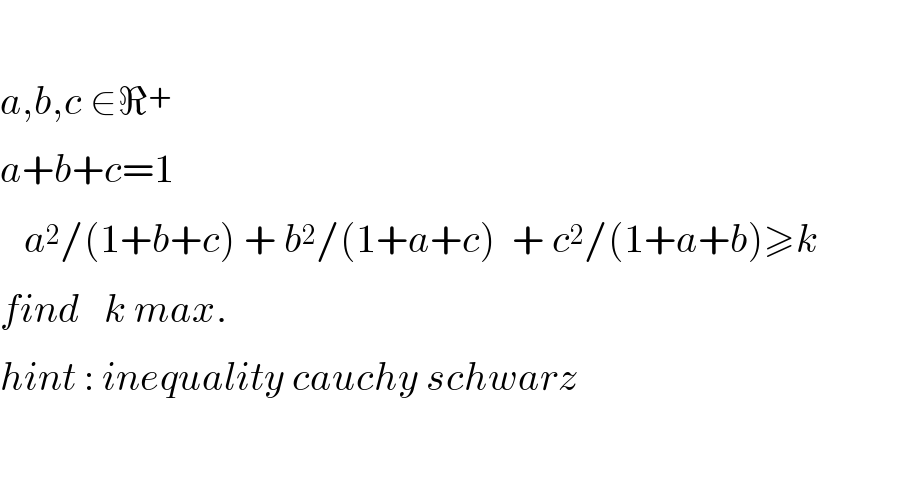
$$ \\ $$$${a},{b},{c}\:\in\Re^{+} \:\: \\ $$$${a}+{b}+{c}=\mathrm{1} \\ $$$$\:\:\:{a}^{\mathrm{2}} /\left(\mathrm{1}+{b}+{c}\right)\:+\:{b}^{\mathrm{2}} /\left(\mathrm{1}+{a}+{c}\right)\:\:+\:{c}^{\mathrm{2}} /\left(\mathrm{1}+{a}+{b}\right)\geqslant{k} \\ $$$${find}\:\:\:{k}\:{max}. \\ $$$${hint}\::\:{inequality}\:{cauchy}\:{schwarz} \\ $$$$ \\ $$
Answered by A5T last updated on 30/Mar/24
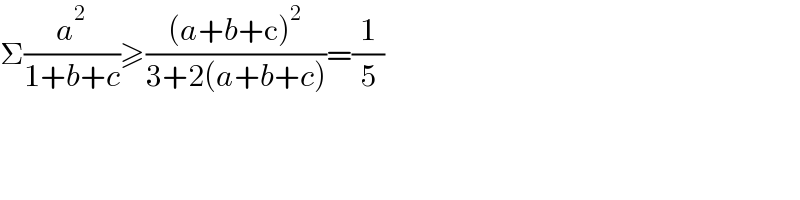
$$\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{b}+{c}}\geqslant\frac{\left({a}+{b}+\mathrm{c}\right)^{\mathrm{2}} }{\mathrm{3}+\mathrm{2}\left({a}+{b}+{c}\right)}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$
Commented by lmcp1203 last updated on 30/Mar/24

$${thanks} \\ $$
