Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10067 by konen last updated on 22/Jan/17

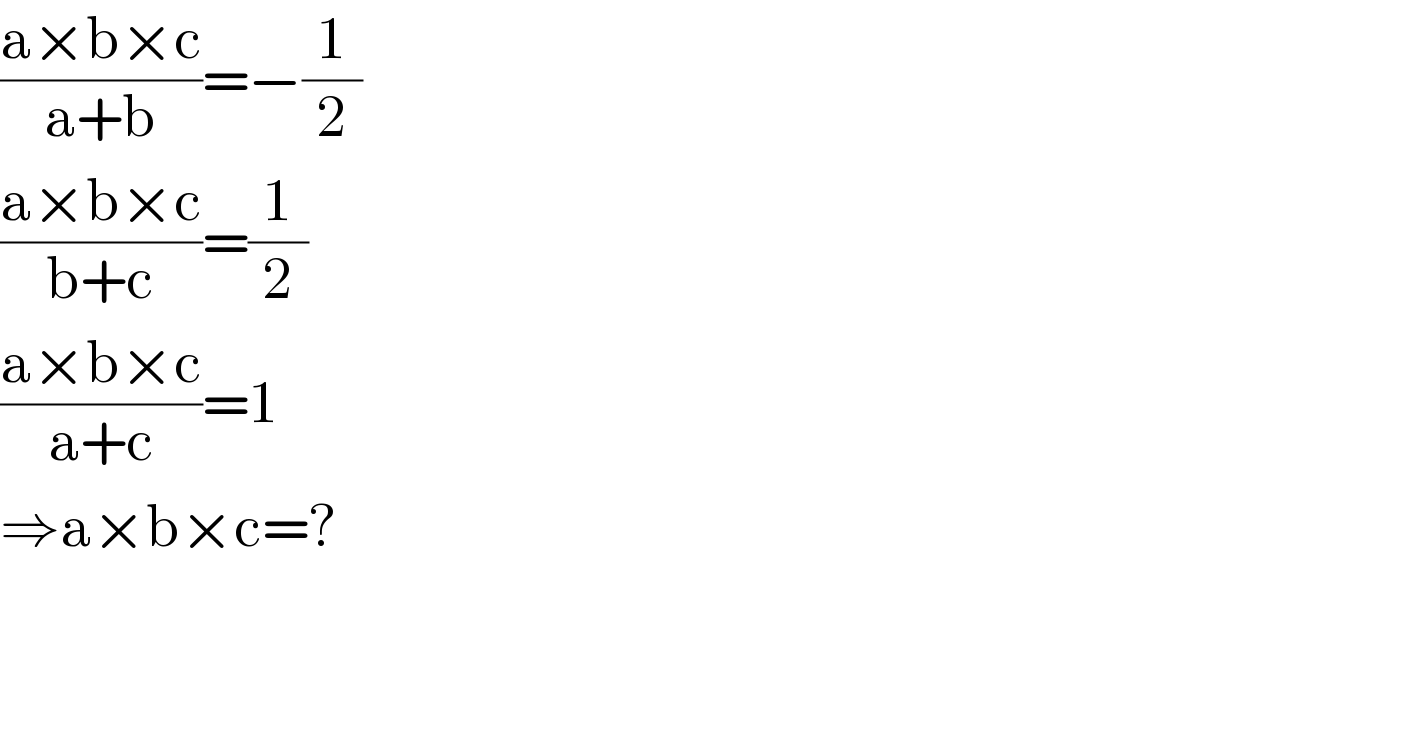
((a×b×c)/(a+b))=−(1/2) ((a×b×c)/(b+c))=(1/2) ((a×b×c)/(a+c))=1 ⇒a×b×c=?

$$\frac{\mathrm{a}×\mathrm{b}×\mathrm{c}}{\mathrm{a}+\mathrm{b}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{a}×\mathrm{b}×\mathrm{c}}{\mathrm{b}+\mathrm{c}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{a}×\mathrm{b}×\mathrm{c}}{\mathrm{a}+\mathrm{c}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}×\mathrm{b}×\mathrm{c}=? \\ $$$$ \\ $$$$ \\ $$

Answered by mrW1 last updated on 22/Jan/17

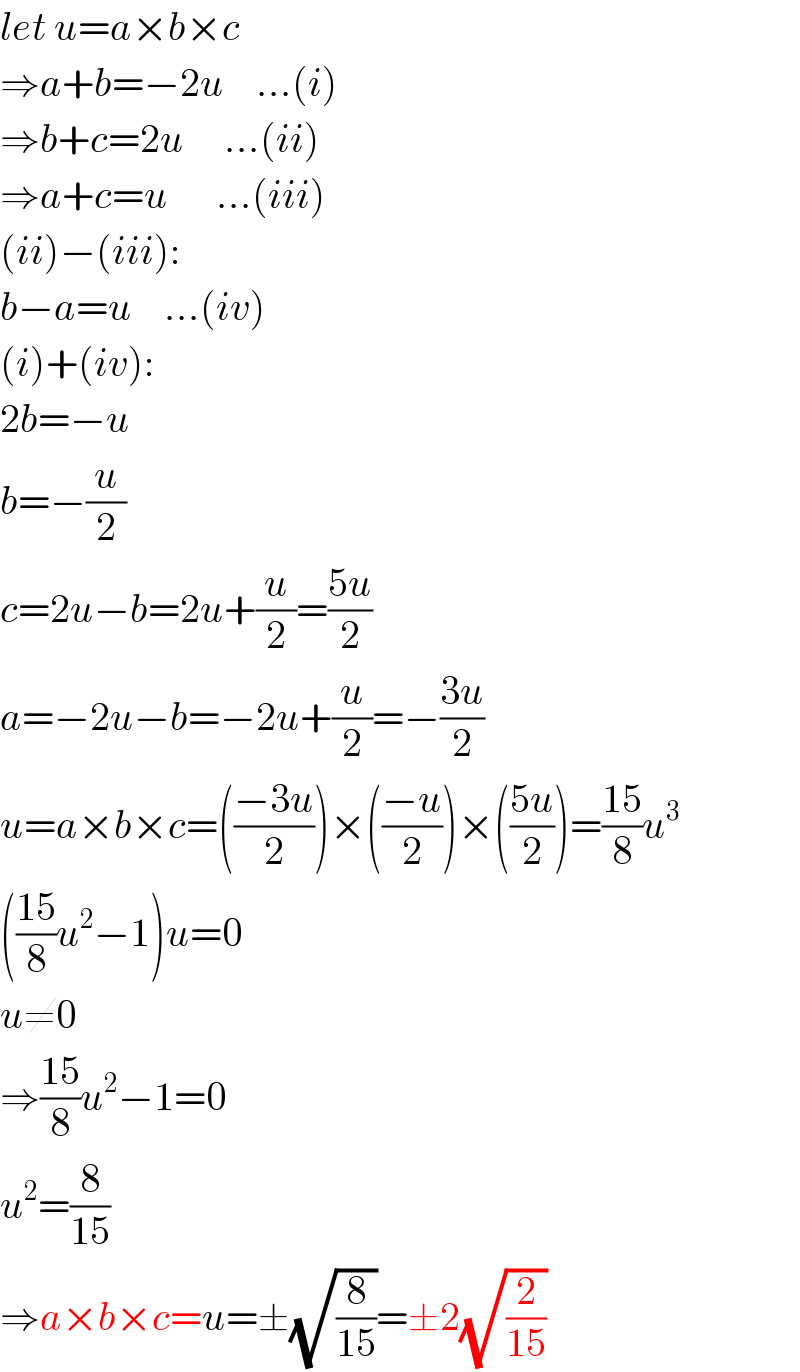
let u=a×b×c ⇒a+b=−2u ...(i) ⇒b+c=2u ...(ii) ⇒a+c=u ...(iii) (ii)−(iii): b−a=u ...(iv) (i)+(iv): 2b=−u b=−(u/2) c=2u−b=2u+(u/2)=((5u)/2) a=−2u−b=−2u+(u/2)=−((3u)/2) u=a×b×c=(((−3u)/2))×(((−u)/2))×(((5u)/2))=((15)/8)u^3 (((15)/8)u^2 −1)u=0 u≠0 ⇒((15)/8)u^2 −1=0 u^2 =(8/(15)) ⇒a×b×c=u=±(√(8/(15)))=±2(√(2/(15)))

$${let}\:{u}={a}×{b}×{c} \\ $$$$\Rightarrow{a}+{b}=−\mathrm{2}{u}\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow{b}+{c}=\mathrm{2}{u}\:\:\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{a}+{c}={u}\:\:\:\:\:\:...\left({iii}\right) \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$${b}−{a}={u}\:\:\:\:...\left({iv}\right) \\ $$$$\left({i}\right)+\left({iv}\right): \\ $$$$\mathrm{2}{b}=−{u} \\ $$$${b}=−\frac{{u}}{\mathrm{2}} \\ $$$${c}=\mathrm{2}{u}−{b}=\mathrm{2}{u}+\frac{{u}}{\mathrm{2}}=\frac{\mathrm{5}{u}}{\mathrm{2}} \\ $$$${a}=−\mathrm{2}{u}−{b}=−\mathrm{2}{u}+\frac{{u}}{\mathrm{2}}=−\frac{\mathrm{3}{u}}{\mathrm{2}} \\ $$$${u}={a}×{b}×{c}=\left(\frac{−\mathrm{3}{u}}{\mathrm{2}}\right)×\left(\frac{−{u}}{\mathrm{2}}\right)×\left(\frac{\mathrm{5}{u}}{\mathrm{2}}\right)=\frac{\mathrm{15}}{\mathrm{8}}{u}^{\mathrm{3}} \\ $$$$\left(\frac{\mathrm{15}}{\mathrm{8}}{u}^{\mathrm{2}} −\mathrm{1}\right){u}=\mathrm{0} \\ $$$${u}\neq\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{15}}{\mathrm{8}}{u}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${u}^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{15}} \\ $$$$\Rightarrow{a}×{b}×{c}={u}=\pm\sqrt{\frac{\mathrm{8}}{\mathrm{15}}}=\pm\mathrm{2}\sqrt{\frac{\mathrm{2}}{\mathrm{15}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com