
Question Number 217958 by dscm last updated on 23/Mar/25
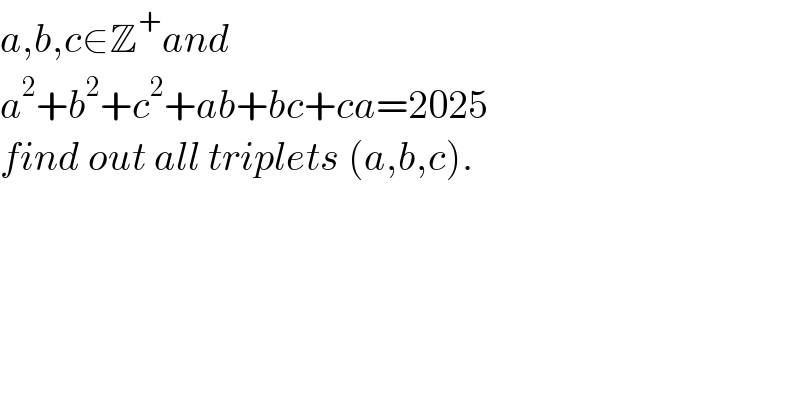
$${a},{b},{c}\in\mathbb{Z}^{+} {and} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ab}+{bc}+{ca}=\mathrm{2025} \\ $$$${find}\:{out}\:{all}\:{triplets}\:\left({a},{b},{c}\right). \\ $$
Commented by Unhombre last updated on 24/Mar/25
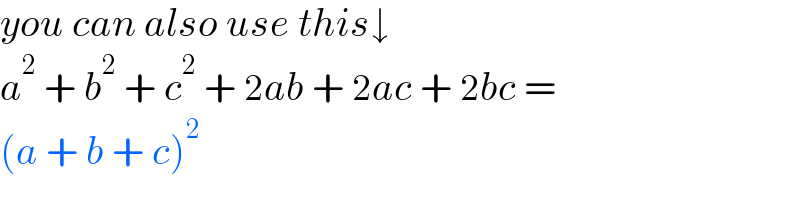
$${you}\:{can}\:{also}\:{use}\:{this}\downarrow \\ $$$${a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:+\:\mathrm{2}{ab}\:+\:\mathrm{2}{ac}\:+\:\mathrm{2}{bc}\:= \\ $$$$\left({a}\:+\:{b}\:+\:{c}\right)^{\mathrm{2}} \\ $$
Commented by Frix last updated on 24/Mar/25
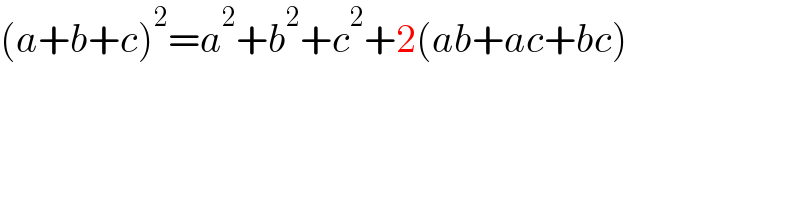
$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{ac}+{bc}\right) \\ $$
Answered by mehdee7396 last updated on 24/Mar/25
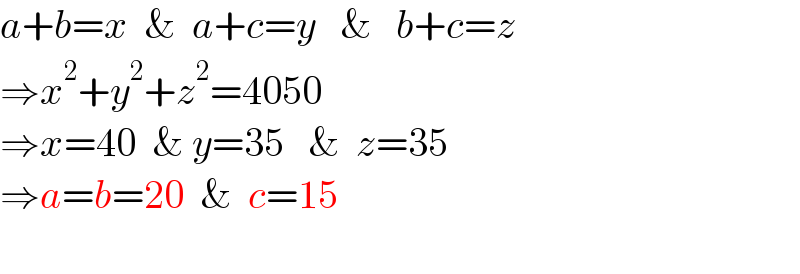
$${a}+{b}={x}\:\:\&\:\:{a}+{c}={y}\:\:\:\&\:\:\:{b}+{c}={z} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{4050} \\ $$$$\Rightarrow{x}=\mathrm{40}\:\:\&\:{y}=\mathrm{35}\:\:\:\&\:\:{z}=\mathrm{35} \\ $$$$\Rightarrow{a}={b}=\mathrm{20}\:\:\&\:\:{c}=\mathrm{15} \\ $$$$ \\ $$
Answered by mahdipoor last updated on 23/Mar/25
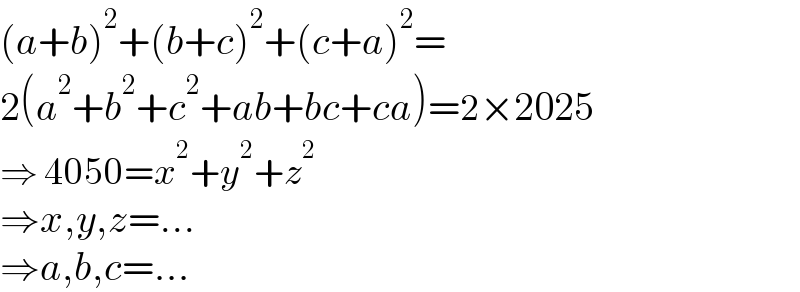
$$\left({a}+{b}\right)^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} +\left({c}+{a}\right)^{\mathrm{2}} = \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ab}+{bc}+{ca}\right)=\mathrm{2}×\mathrm{2025} \\ $$$$\Rightarrow\:\mathrm{4050}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \\ $$$$\Rightarrow{x},{y},{z}=... \\ $$$$\Rightarrow{a},{b},{c}=... \\ $$
