Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 204621 by hardmath last updated on 23/Feb/24

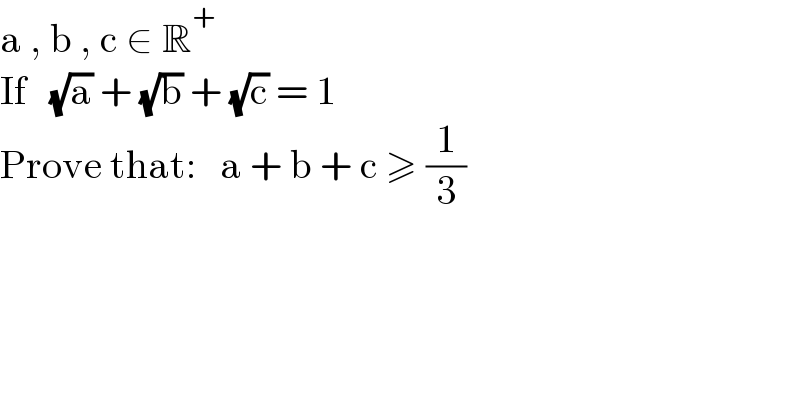
a , b , c ∈ R^+ If (√a) + (√b) + (√c) = 1 Prove that: a + b + c ≥ (1/3)

$$\mathrm{a}\:,\:\mathrm{b}\:,\:\mathrm{c}\:\in\:\mathbb{R}^{+} \\ $$$$\mathrm{If}\:\:\:\sqrt{\mathrm{a}}\:+\:\sqrt{\mathrm{b}}\:+\:\sqrt{\mathrm{c}}\:=\:\mathrm{1} \\ $$$$\mathrm{Prove}\:\mathrm{that}:\:\:\:\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Answered by A5T last updated on 23/Feb/24

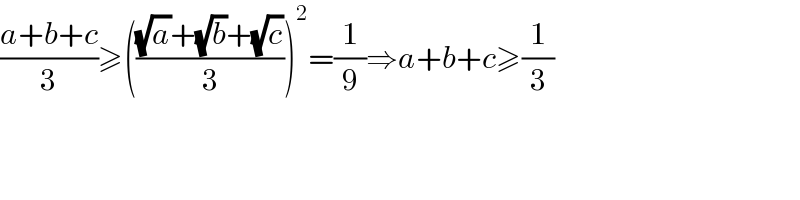
((a+b+c)/3)≥((((√a)+(√b)+(√c))/3))^2 =(1/9)⇒a+b+c≥(1/3)

$$\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\left(\frac{\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{9}}\Rightarrow{a}+{b}+{c}\geqslant\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Answered by mr W last updated on 23/Feb/24

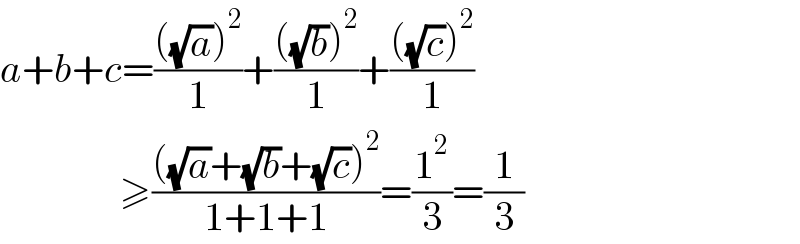
a+b+c=((((√a))^2 )/1)+((((√b))^2 )/1)+((((√c))^2 )/1) ≥((((√a)+(√b)+(√c))^2 )/(1+1+1))=(1^2 /3)=(1/3)

$${a}+{b}+{c}=\frac{\left(\sqrt{{a}}\right)^{\mathrm{2}} }{\mathrm{1}}+\frac{\left(\sqrt{{b}}\right)^{\mathrm{2}} }{\mathrm{1}}+\frac{\left(\sqrt{{c}}\right)^{\mathrm{2}} }{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant\frac{\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{1}+\mathrm{1}}=\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by mr W last updated on 23/Feb/24

Answered by mr W last updated on 24/Feb/24

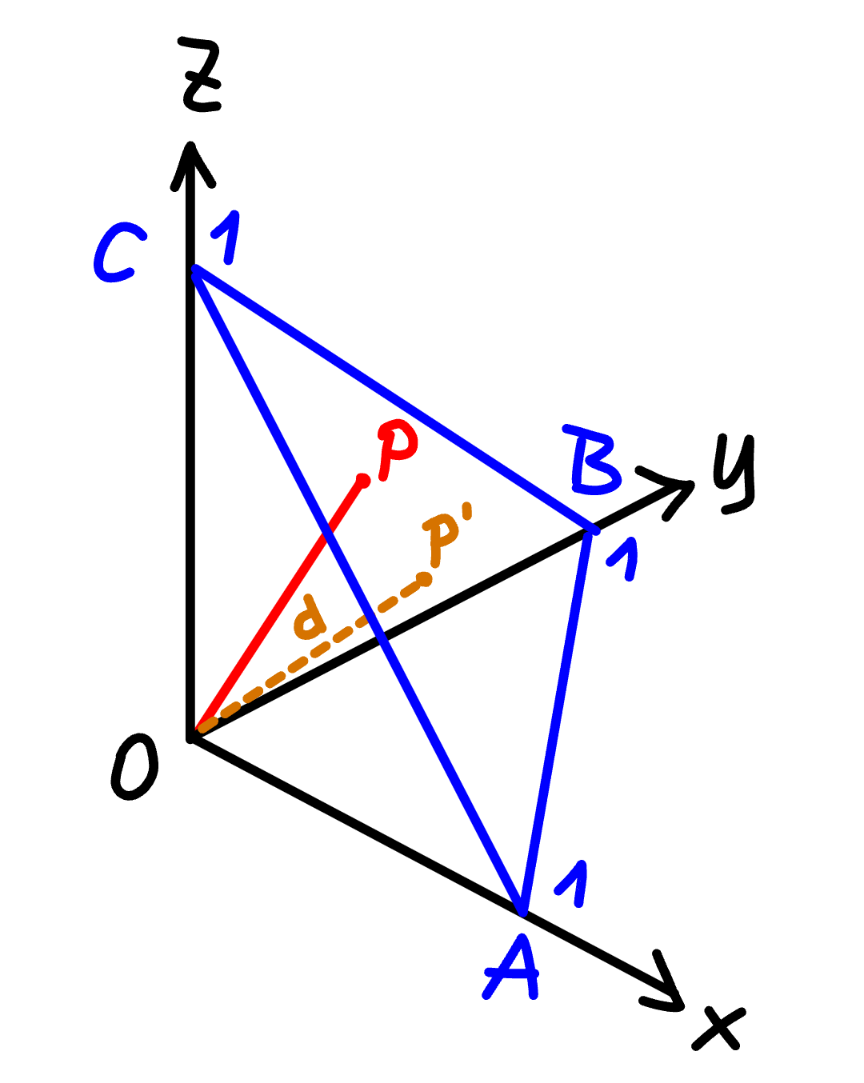
Commented by mr W last updated on 24/Feb/24

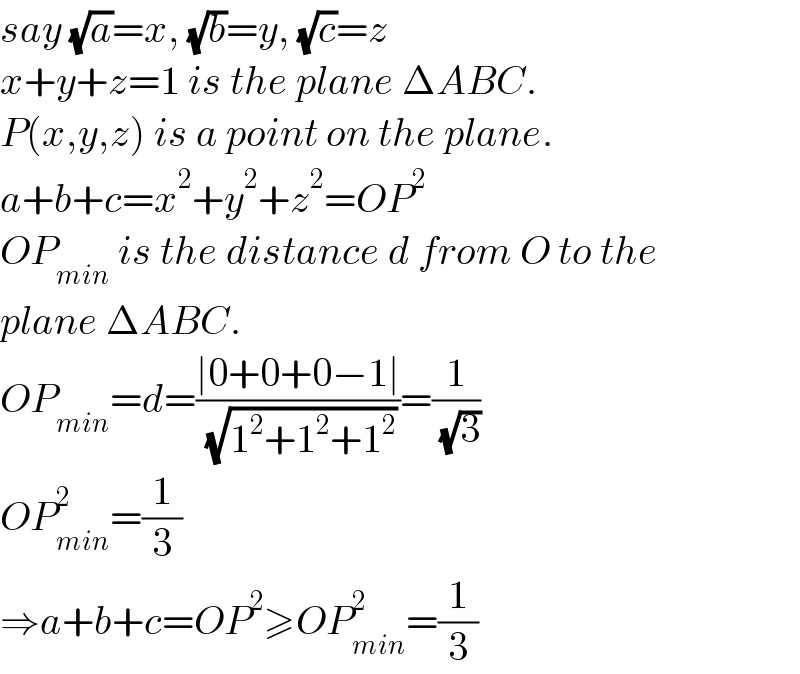
say (√a)=x, (√b)=y, (√c)=z x+y+z=1 is the plane ΔABC. P(x,y,z) is a point on the plane. a+b+c=x^2 +y^2 +z^2 =OP^2 OP_(min) is the distance d from O to the plane ΔABC. OP_(min) =d=((∣0+0+0−1∣)/( (√(1^2 +1^2 +1^2 ))))=(1/( (√3))) OP_(min) ^2 =(1/3) ⇒a+b+c=OP^2 ≥OP_(min) ^2 =(1/3)

$${say}\:\sqrt{{a}}={x},\:\sqrt{{b}}={y},\:\sqrt{{c}}={z} \\ $$$${x}+{y}+{z}=\mathrm{1}\:{is}\:{the}\:{plane}\:\Delta{ABC}. \\ $$$${P}\left({x},{y},{z}\right)\:{is}\:{a}\:{point}\:{on}\:{the}\:{plane}. \\ $$$${a}+{b}+{c}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={OP}^{\mathrm{2}} \\ $$$${OP}_{{min}} \:{is}\:{the}\:{distance}\:{d}\:{from}\:{O}\:{to}\:{the} \\ $$$${plane}\:\Delta{ABC}. \\ $$$${OP}_{{min}} ={d}=\frac{\mid\mathrm{0}+\mathrm{0}+\mathrm{0}−\mathrm{1}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${OP}_{{min}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{a}+{b}+{c}={OP}^{\mathrm{2}} \geqslant{OP}_{{min}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by hardmath last updated on 24/Feb/24

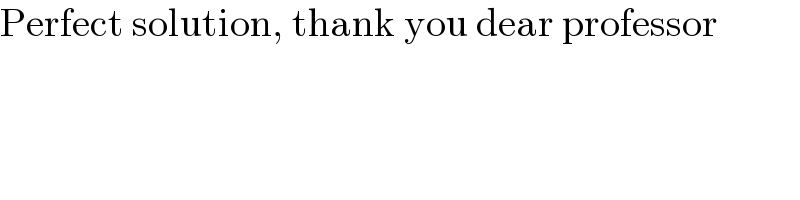
Perfect solution, thank you dear professor

$$\mathrm{Perfect}\:\mathrm{solution},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com