Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139051 by mathsuji last updated on 21/Apr/21

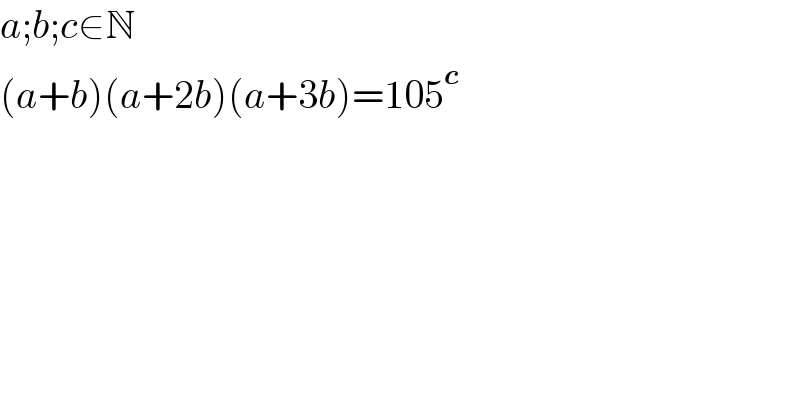
a;b;c∈N (a+b)(a+2b)(a+3b)=105^c

$${a};{b};{c}\in\mathbb{N} \\ $$$$\left({a}+{b}\right)\left({a}+\mathrm{2}{b}\right)\left({a}+\mathrm{3}{b}\right)=\mathrm{105}^{\boldsymbol{{c}}} \\ $$

Commented by Rasheed.Sindhi last updated on 22/Apr/21

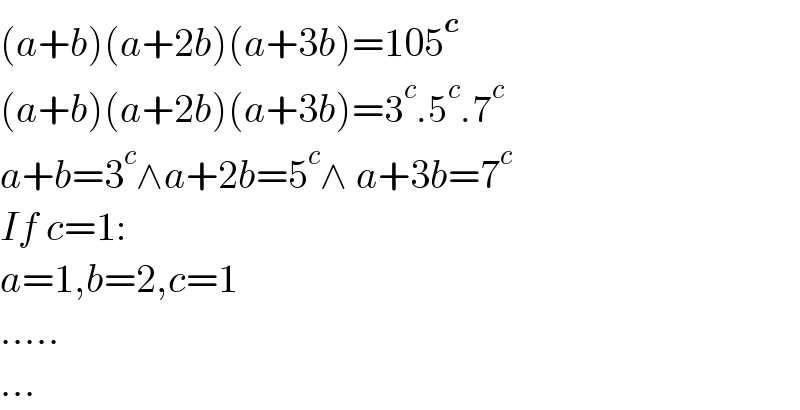
(a+b)(a+2b)(a+3b)=105^c (a+b)(a+2b)(a+3b)=3^c .5^c .7^c a+b=3^c ∧a+2b=5^c ∧ a+3b=7^c If c=1: a=1,b=2,c=1 ..... ...

$$\left({a}+{b}\right)\left({a}+\mathrm{2}{b}\right)\left({a}+\mathrm{3}{b}\right)=\mathrm{105}^{\boldsymbol{{c}}} \\ $$$$\left({a}+{b}\right)\left({a}+\mathrm{2}{b}\right)\left({a}+\mathrm{3}{b}\right)=\mathrm{3}^{{c}} .\mathrm{5}^{{c}} .\mathrm{7}^{{c}} \\ $$$${a}+{b}=\mathrm{3}^{{c}} \wedge{a}+\mathrm{2}{b}=\mathrm{5}^{{c}} \wedge\:{a}+\mathrm{3}{b}=\mathrm{7}^{{c}} \\ $$$${If}\:{c}=\mathrm{1}: \\ $$$${a}=\mathrm{1},{b}=\mathrm{2},{c}=\mathrm{1} \\ $$$$..... \\ $$$$... \\ $$

Commented by mathsuji last updated on 22/Apr/21

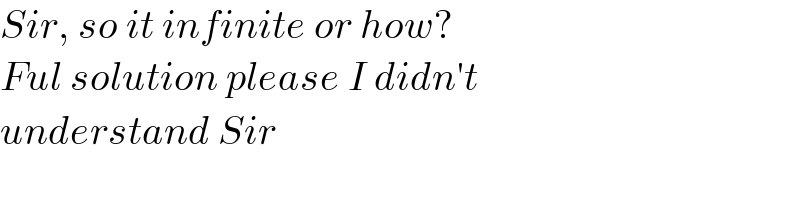
Sir, so it infinite or how? Ful solution please I didn′t understand Sir

$${Sir},\:{so}\:{it}\:{infinite}\:{or}\:{how}? \\ $$$${Ful}\:{solution}\:{please}\:{I}\:{didn}'{t} \\ $$$${understand}\:{Sir} \\ $$

Commented by Rasheed.Sindhi last updated on 22/Apr/21

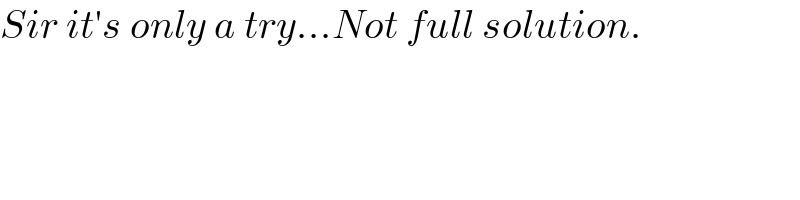
Sir it′s only a try...Not full solution.

$${Sir}\:{it}'{s}\:{only}\:{a}\:{try}...{Not}\:{full}\:{solution}. \\ $$

Commented by mathdanisur last updated on 24/Apr/21

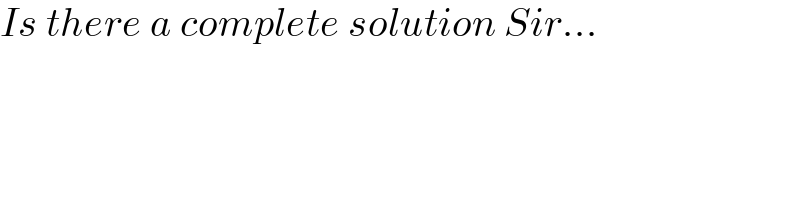
Is there a complete solution Sir...

$${Is}\:{there}\:{a}\:{complete}\:{solution}\:{Sir}... \\ $$

Commented by Rasheed.Sindhi last updated on 25/Apr/21

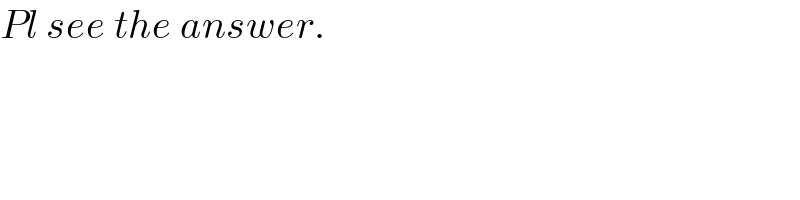
Pl see the answer.

$${Pl}\:{see}\:{the}\:{answer}. \\ $$

Answered by Rasheed.Sindhi last updated on 25/Apr/21

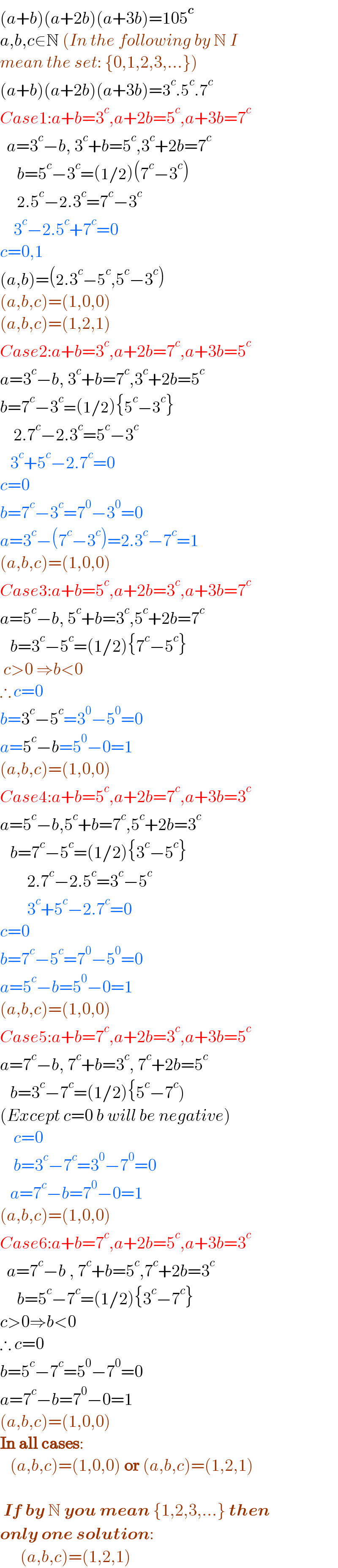
(a+b)(a+2b)(a+3b)=105^c a,b,c∈N (In the following by N I mean the set: {0,1,2,3,...}) (a+b)(a+2b)(a+3b)=3^c .5^c .7^c Case1:a+b=3^c ,a+2b=5^c ,a+3b=7^c a=3^c −b, 3^c +b=5^c ,3^c +2b=7^c b=5^c −3^c =(1/2)(7^c −3^c ) 2.5^c −2.3^c =7^c −3^c 3^c −2.5^c +7^c =0 c=0,1 (a,b)=(2.3^c −5^c ,5^c −3^c ) (a,b,c)=(1,0,0) (a,b,c)=(1,2,1) Case2:a+b=3^c ,a+2b=7^c ,a+3b=5^c a=3^c −b, 3^c +b=7^c ,3^c +2b=5^c b=7^c −3^c =(1/2){5^c −3^c } 2.7^c −2.3^c =5^c −3^c 3^c +5^c −2.7^c =0 c=0 b=7^c −3^c =7^0 −3^0 =0 a=3^c −(7^c −3^c )=2.3^c −7^c =1 (a,b,c)=(1,0,0) Case3:a+b=5^c ,a+2b=3^c ,a+3b=7^c a=5^c −b, 5^c +b=3^c ,5^c +2b=7^c b=3^c −5^c =(1/2){7^c −5^c } c>0 ⇒b<0 ∴ c=0 b=3^c −5^c =3^0 −5^0 =0 a=5^c −b=5^0 −0=1 (a,b,c)=(1,0,0) Case4:a+b=5^c ,a+2b=7^c ,a+3b=3^c a=5^c −b,5^c +b=7^c ,5^c +2b=3^c b=7^c −5^c =(1/2){3^c −5^c } 2.7^c −2.5^c =3^c −5^c 3^c +5^c −2.7^c =0 c=0 b=7^c −5^c =7^0 −5^0 =0 a=5^c −b=5^0 −0=1 (a,b,c)=(1,0,0) Case5:a+b=7^c ,a+2b=3^c ,a+3b=5^c a=7^c −b, 7^c +b=3^c , 7^c +2b=5^c b=3^c −7^c =(1/2){5^c −7^c ) (Except c=0 b will be negative) c=0 b=3^c −7^c =3^0 −7^0 =0 a=7^c −b=7^0 −0=1 (a,b,c)=(1,0,0) Case6:a+b=7^c ,a+2b=5^c ,a+3b=3^c a=7^c −b , 7^c +b=5^c ,7^c +2b=3^c b=5^c −7^c =(1/2){3^c −7^c } c>0⇒b<0 ∴ c=0 b=5^c −7^c =5^0 −7^0 =0 a=7^c −b=7^0 −0=1 (a,b,c)=(1,0,0) In all cases: (a,b,c)=(1,0,0) or (a,b,c)=(1,2,1) If by N you mean {1,2,3,...} then only one solution: (a,b,c)=(1,2,1)

$$\left({a}+{b}\right)\left({a}+\mathrm{2}{b}\right)\left({a}+\mathrm{3}{b}\right)=\mathrm{105}^{\boldsymbol{{c}}} \\ $$$${a},{b},{c}\in\mathbb{N}\:\left({In}\:{the}\:{following}\:{by}\:\mathbb{N}\:{I}\:\right. \\ $$$$\left.{mean}\:{the}\:{set}:\:\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},...\right\}\right) \\ $$$$\left({a}+{b}\right)\left({a}+\mathrm{2}{b}\right)\left({a}+\mathrm{3}{b}\right)=\mathrm{3}^{{c}} .\mathrm{5}^{{c}} .\mathrm{7}^{{c}} \\ $$$${Case}\mathrm{1}:{a}+{b}=\mathrm{3}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{5}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{7}^{{c}} \\ $$$$\:\:{a}=\mathrm{3}^{{c}} −{b},\:\mathrm{3}^{{c}} +{b}=\mathrm{5}^{{c}} ,\mathrm{3}^{{c}} +\mathrm{2}{b}=\mathrm{7}^{{c}} \\ $$$$\:\:\:\:\:{b}=\mathrm{5}^{{c}} −\mathrm{3}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left(\mathrm{7}^{{c}} −\mathrm{3}^{{c}} \right) \\ $$$$\:\:\:\:\:\mathrm{2}.\mathrm{5}^{{c}} −\mathrm{2}.\mathrm{3}^{{c}} =\mathrm{7}^{{c}} −\mathrm{3}^{{c}} \\ $$$$\:\:\:\:\mathrm{3}^{{c}} −\mathrm{2}.\mathrm{5}^{{c}} +\mathrm{7}^{{c}} =\mathrm{0} \\ $$$${c}=\mathrm{0},\mathrm{1}\: \\ $$$$\left({a},{b}\right)=\left(\mathrm{2}.\mathrm{3}^{{c}} −\mathrm{5}^{{c}} ,\mathrm{5}^{{c}} −\mathrm{3}^{{c}} \right) \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{2},\mathrm{1}\right) \\ $$$${Case}\mathrm{2}:{a}+{b}=\mathrm{3}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{7}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{5}^{{c}} \\ $$$${a}=\mathrm{3}^{{c}} −{b},\:\mathrm{3}^{{c}} +{b}=\mathrm{7}^{{c}} ,\mathrm{3}^{{c}} +\mathrm{2}{b}=\mathrm{5}^{{c}} \\ $$$${b}=\mathrm{7}^{{c}} −\mathrm{3}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left\{\mathrm{5}^{{c}} −\mathrm{3}^{{c}} \right\} \\ $$$$\:\:\:\:\mathrm{2}.\mathrm{7}^{{c}} −\mathrm{2}.\mathrm{3}^{{c}} =\mathrm{5}^{{c}} −\mathrm{3}^{{c}} \\ $$$$\:\:\:\mathrm{3}^{{c}} +\mathrm{5}^{{c}} −\mathrm{2}.\mathrm{7}^{{c}} =\mathrm{0} \\ $$$${c}=\mathrm{0} \\ $$$${b}=\mathrm{7}^{{c}} −\mathrm{3}^{{c}} =\mathrm{7}^{\mathrm{0}} −\mathrm{3}^{\mathrm{0}} =\mathrm{0} \\ $$$${a}=\mathrm{3}^{{c}} −\left(\mathrm{7}^{{c}} −\mathrm{3}^{{c}} \right)=\mathrm{2}.\mathrm{3}^{{c}} −\mathrm{7}^{{c}} =\mathrm{1} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$${Case}\mathrm{3}:{a}+{b}=\mathrm{5}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{3}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{7}^{{c}} \\ $$$${a}=\mathrm{5}^{{c}} −{b},\:\mathrm{5}^{{c}} +{b}=\mathrm{3}^{{c}} ,\mathrm{5}^{{c}} +\mathrm{2}{b}=\mathrm{7}^{{c}} \\ $$$$\:\:\:{b}=\mathrm{3}^{{c}} −\mathrm{5}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left\{\mathrm{7}^{{c}} −\mathrm{5}^{{c}} \right\} \\ $$$$\:{c}>\mathrm{0}\:\Rightarrow{b}<\mathrm{0} \\ $$$$\therefore\:{c}=\mathrm{0} \\ $$$${b}=\mathrm{3}^{{c}} −\mathrm{5}^{{c}} =\mathrm{3}^{\mathrm{0}} −\mathrm{5}^{\mathrm{0}} =\mathrm{0} \\ $$$${a}=\mathrm{5}^{{c}} −{b}=\mathrm{5}^{\mathrm{0}} −\mathrm{0}=\mathrm{1} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$${Case}\mathrm{4}:{a}+{b}=\mathrm{5}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{7}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{3}^{{c}} \\ $$$${a}=\mathrm{5}^{{c}} −{b},\mathrm{5}^{{c}} +{b}=\mathrm{7}^{{c}} ,\mathrm{5}^{{c}} +\mathrm{2}{b}=\mathrm{3}^{{c}} \\ $$$$\:\:\:{b}=\mathrm{7}^{{c}} −\mathrm{5}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left\{\mathrm{3}^{{c}} −\mathrm{5}^{{c}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}.\mathrm{7}^{{c}} −\mathrm{2}.\mathrm{5}^{{c}} =\mathrm{3}^{{c}} −\mathrm{5}^{{c}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{3}^{{c}} +\mathrm{5}^{{c}} −\mathrm{2}.\mathrm{7}^{{c}} =\mathrm{0} \\ $$$${c}=\mathrm{0} \\ $$$${b}=\mathrm{7}^{{c}} −\mathrm{5}^{{c}} =\mathrm{7}^{\mathrm{0}} −\mathrm{5}^{\mathrm{0}} =\mathrm{0} \\ $$$${a}=\mathrm{5}^{{c}} −{b}=\mathrm{5}^{\mathrm{0}} −\mathrm{0}=\mathrm{1} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$${Case}\mathrm{5}:{a}+{b}=\mathrm{7}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{3}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{5}^{{c}} \\ $$$${a}=\mathrm{7}^{{c}} −{b},\:\mathrm{7}^{{c}} +{b}=\mathrm{3}^{{c}} ,\:\mathrm{7}^{{c}} +\mathrm{2}{b}=\mathrm{5}^{{c}} \\ $$$$\:\:\:{b}=\mathrm{3}^{{c}} −\mathrm{7}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left\{\mathrm{5}^{{c}} −\mathrm{7}^{{c}} \right) \\ $$$$\left({Except}\:{c}=\mathrm{0}\:{b}\:{will}\:{be}\:{negative}\right) \\ $$$$\:\:\:\:{c}=\mathrm{0} \\ $$$$\:\:\:\:{b}=\mathrm{3}^{{c}} −\mathrm{7}^{{c}} =\mathrm{3}^{\mathrm{0}} −\mathrm{7}^{\mathrm{0}} =\mathrm{0} \\ $$$$\:\:\:{a}=\mathrm{7}^{{c}} −{b}=\mathrm{7}^{\mathrm{0}} −\mathrm{0}=\mathrm{1} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$${Case}\mathrm{6}:{a}+{b}=\mathrm{7}^{{c}} ,{a}+\mathrm{2}{b}=\mathrm{5}^{{c}} ,{a}+\mathrm{3}{b}=\mathrm{3}^{{c}} \\ $$$$\:\:{a}=\mathrm{7}^{{c}} −{b}\:,\:\mathrm{7}^{{c}} +{b}=\mathrm{5}^{{c}} ,\mathrm{7}^{{c}} +\mathrm{2}{b}=\mathrm{3}^{{c}} \\ $$$$\:\:\:\:\:{b}=\mathrm{5}^{{c}} −\mathrm{7}^{{c}} =\left(\mathrm{1}/\mathrm{2}\right)\left\{\mathrm{3}^{{c}} −\mathrm{7}^{{c}} \right\} \\ $$$${c}>\mathrm{0}\Rightarrow{b}<\mathrm{0} \\ $$$$\therefore\:{c}=\mathrm{0} \\ $$$${b}=\mathrm{5}^{{c}} −\mathrm{7}^{{c}} =\mathrm{5}^{\mathrm{0}} −\mathrm{7}^{\mathrm{0}} =\mathrm{0} \\ $$$${a}=\mathrm{7}^{{c}} −{b}=\mathrm{7}^{\mathrm{0}} −\mathrm{0}=\mathrm{1} \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right) \\ $$$$\boldsymbol{\mathrm{In}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{cases}}: \\ $$$$\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right)\:\boldsymbol{\mathrm{or}}\:\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{2},\mathrm{1}\right) \\ $$$$ \\ $$$$\:\boldsymbol{{If}}\:\boldsymbol{{by}}\:\mathbb{N}\:\boldsymbol{{you}}\:\boldsymbol{{mean}}\:\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\}\:\boldsymbol{{then}} \\ $$$$\boldsymbol{{only}}\:\boldsymbol{{one}}\:\boldsymbol{{solution}}: \\ $$$$\:\:\:\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{1},\mathrm{2},\mathrm{1}\right) \\ $$

Commented by mathsuji last updated on 28/Apr/21

cool thanks sir

$${cool}\:{thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com