Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 220468 by Rojarani last updated on 13/May/25

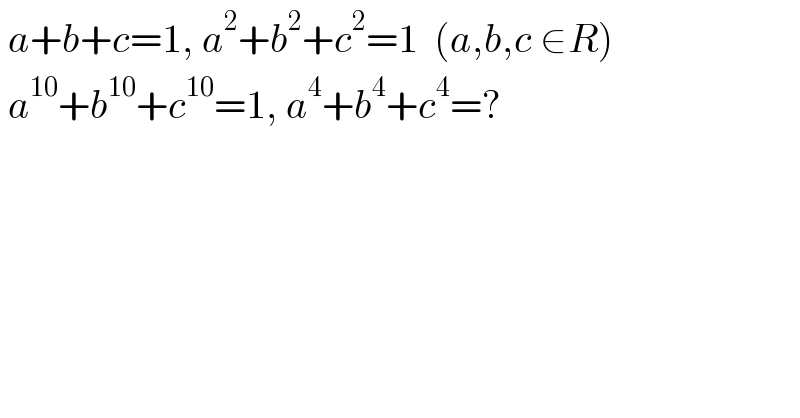
a+b+c=1, a^2 +b^2 +c^2 =1 (a,b,c ∈R) a^(10) +b^(10) +c^(10) =1, a^4 +b^4 +c^4 =?

$$\:{a}+{b}+{c}=\mathrm{1},\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{1}\:\:\left({a},{b},{c}\:\in{R}\right) \\ $$$$\:{a}^{\mathrm{10}} +{b}^{\mathrm{10}} +{c}^{\mathrm{10}} =\mathrm{1},\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =? \\ $$

Answered by mr W last updated on 15/May/25

say abc=k (a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ca) 1^2 =1+2(ab+bc+ca) ⇒ab+bc+ca=0 (ab+bc+ca)^2 =a^2 b^2 +b^2 c^2 +c^2 a^2 +2abc(a+b+c) ⇒a^2 b^2 +b^2 c^2 +c^2 a^2 =−2k a^4 b^4 +b^4 c^4 +c^4 a^4 +2(abc)^2 (a^2 +b^2 +c^2 )=4k^2 ⇒a^4 b^4 +b^4 c^4 +c^4 a^4 =2k^2 (a^2 +b^2 +c^2 )^2 =a^4 +b^4 +c^4 +2(a^2 b^2 +b^2 c^2 +c^2 a^2 ) ⇒a^4 +b^4 +c^4 =1+4k (a^4 +b^4 +c^4 )(a^2 +b^2 +c^2 )=1+4k a^6 +b^6 +c^6 +(a^2 +b^2 +c^2 )(a^2 b^2 +b^2 c^2 +c^2 a^2 )−3(abc)^2 =1+4k ⇒a^6 +b^6 +c^6 =1+6k+3k^2 (a^6 +b^6 +c^6 )(a^4 +b^4 +c^4 )=(1+6k+3k^2 )(1+4k) a^(10) +b^(10) +c^(10) +(a^2 +b^2 +c^2 )(a^4 b^4 +b^4 c^4 +c^4 a^4 )−3(abc)^2 =(1+6k+3k^2 )(1+4k) 1+2k^2 −3k^2 =(1+6k+3k^2 )(1+4k) k(6k^2 +14k+5)=0 ⇒k=0 or ((−7±(√(19)))/6) a^4 +b^4 +c^4 =1+4k=1 or ((−11±2(√(19)))/3) if a, b, c ∈ R, then ((−11±2(√(19)))/3)<0 must be rejected.

$${say}\:{abc}={k} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\mathrm{1}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\Rightarrow{ab}+{bc}+{ca}=\mathrm{0} \\ $$$$\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{2}{abc}\left({a}+{b}+{c}\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} =−\mathrm{2}{k} \\ $$$${a}^{\mathrm{4}} {b}^{\mathrm{4}} +{b}^{\mathrm{4}} {c}^{\mathrm{4}} +{c}^{\mathrm{4}} {a}^{\mathrm{4}} +\mathrm{2}\left({abc}\right)^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\mathrm{4}{k}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{4}} {b}^{\mathrm{4}} +{b}^{\mathrm{4}} {c}^{\mathrm{4}} +{c}^{\mathrm{4}} {a}^{\mathrm{4}} =\mathrm{2}{k}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} ={a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} +\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\mathrm{1}+\mathrm{4}{k} \\ $$$$\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\mathrm{1}+\mathrm{4}{k} \\ $$$${a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\mathrm{3}\left({abc}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{4}{k} \\ $$$$\Rightarrow{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} =\mathrm{1}+\mathrm{6}{k}+\mathrm{3}{k}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} \right)\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)=\left(\mathrm{1}+\mathrm{6}{k}+\mathrm{3}{k}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{k}\right) \\ $$$${a}^{\mathrm{10}} +{b}^{\mathrm{10}} +{c}^{\mathrm{10}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}^{\mathrm{4}} {b}^{\mathrm{4}} +{b}^{\mathrm{4}} {c}^{\mathrm{4}} +{c}^{\mathrm{4}} {a}^{\mathrm{4}} \right)−\mathrm{3}\left({abc}\right)^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{6}{k}+\mathrm{3}{k}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{k}\right) \\ $$$$\mathrm{1}+\mathrm{2}{k}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{6}{k}+\mathrm{3}{k}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{k}\right) \\ $$$${k}\left(\mathrm{6}{k}^{\mathrm{2}} +\mathrm{14}{k}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{k}=\mathrm{0}\:{or}\:\frac{−\mathrm{7}\pm\sqrt{\mathrm{19}}}{\mathrm{6}} \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\mathrm{1}+\mathrm{4}{k}=\mathrm{1}\:{or}\:\frac{−\mathrm{11}\pm\mathrm{2}\sqrt{\mathrm{19}}}{\mathrm{3}} \\ $$$${if}\:{a},\:{b},\:{c}\:\in\:{R},\:{then}\:\frac{−\mathrm{11}\pm\mathrm{2}\sqrt{\mathrm{19}}}{\mathrm{3}}<\mathrm{0}\: \\ $$$${must}\:{be}\:{rejected}. \\ $$

Commented by Rojarani last updated on 13/May/25

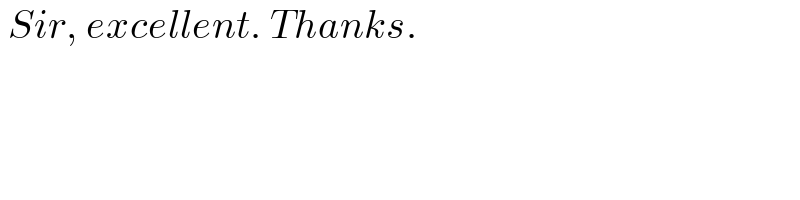
Sir, excellent. Thanks.

$$\:{Sir},\:{excellent}.\:{Thanks}. \\ $$

Commented by Rojarani last updated on 15/May/25

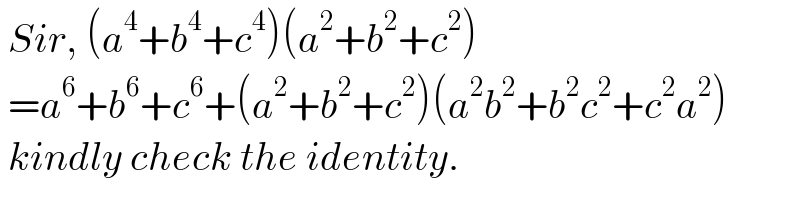
Sir, (a^4 +b^4 +c^4 )(a^2 +b^2 +c^2 ) =a^6 +b^6 +c^6 +(a^2 +b^2 +c^2 )(a^2 b^2 +b^2 c^2 +c^2 a^2 ) kindly check the identity.

$$\:{Sir},\:\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:={a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right) \\ $$$$\:{kindly}\:{check}\:{the}\:{identity}. \\ $$

Commented by mr W last updated on 15/May/25

fixed! thanks for checking!

$${fixed}!\:{thanks}\:{for}\:{checking}! \\ $$

Commented by Rojarani last updated on 15/May/25

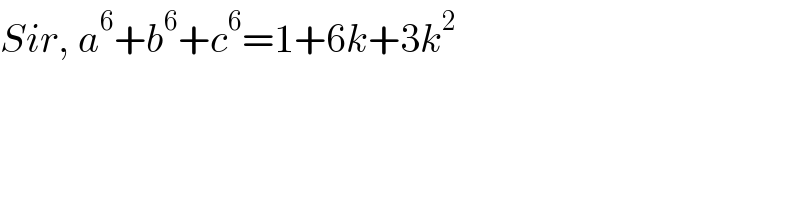
Sir, a^6 +b^6 +c^6 =1+6k+3k^2

$${Sir},\:{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} =\mathrm{1}+\mathrm{6}{k}+\mathrm{3}{k}^{\mathrm{2}} \\ $$

Answered by MrGaster last updated on 13/May/25

{ ((a+b+c=1)),((a^2 +b^2 +c^2 =1)),((a^(10) +b^(10) +c^(10) =1)) :} S_1 =a+b+c=1 S_2 =a^2 +b^2 +c^2 =1 S_(10) =a^(10) +b^(10) +c^(10) =1 Using the symmetric polynomial relations: S_2 =S_1 ^2 −2(ab−bc+ca) 1=1^2 −2(ab+bc+ca) ab+bc+ca=0 Recursive formula for higher-order symmetric sums: S_3 =S_1 ∙S_2 −(ab+bc+ca)∙S_1 +3abc=1+3abc S_4 =S_1 ∙S_3 −(ab+bc+ca)∙S_2 +abc∙S_1 =1+4abc We know that S_1 =1 and S_2 =1,so: S_3 =1+3abc=1⇒abc=0 Now,we need to find S_4 : S_4 =1+4abc=1+4∙0=1 Therefore,the value of a^4 +b^4 +c^4 is 1

$$\begin{cases}{{a}+{b}+{c}=\mathrm{1}}\\{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{1}}\\{{a}^{\mathrm{10}} +{b}^{\mathrm{10}} +{c}^{\mathrm{10}} =\mathrm{1}}\end{cases} \\ $$$${S}_{\mathrm{1}} ={a}+{b}+{c}=\mathrm{1} \\ $$$${S}_{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{1} \\ $$$${S}_{\mathrm{10}} ={a}^{\mathrm{10}} +{b}^{\mathrm{10}} +{c}^{\mathrm{10}} =\mathrm{1} \\ $$$$\mathrm{Using}\:\mathrm{the}\:\mathrm{symmetric}\:\mathrm{polynomial}\:\mathrm{relations}: \\ $$$${S}_{\mathrm{2}} ={S}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}\left({ab}−{bc}+{ca}\right) \\ $$$$\mathrm{1}=\mathrm{1}^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${ab}+{bc}+{ca}=\mathrm{0} \\ $$$$\mathrm{Recursive}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{higher}-\mathrm{order}\:\mathrm{symmetric}\:\mathrm{sums}: \\ $$$${S}_{\mathrm{3}} ={S}_{\mathrm{1}} \centerdot{S}_{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)\centerdot{S}_{\mathrm{1}} +\mathrm{3}{abc}=\mathrm{1}+\mathrm{3}{abc} \\ $$$${S}_{\mathrm{4}} ={S}_{\mathrm{1}} \centerdot{S}_{\mathrm{3}} −\left({ab}+{bc}+{ca}\right)\centerdot{S}_{\mathrm{2}} +{abc}\centerdot{S}_{\mathrm{1}} =\mathrm{1}+\mathrm{4}{abc} \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{that}\:{S}_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:{S}_{\mathrm{2}} =\mathrm{1},\mathrm{so}: \\ $$$${S}_{\mathrm{3}} =\mathrm{1}+\mathrm{3}{abc}=\mathrm{1}\Rightarrow{abc}=\mathrm{0} \\ $$$$\mathrm{Now},\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:{S}_{\mathrm{4}} : \\ $$$${S}_{\mathrm{4}} =\mathrm{1}+\mathrm{4}{abc}=\mathrm{1}+\mathrm{4}\centerdot\mathrm{0}=\mathrm{1} \\ $$$$\mathrm{Therefore},\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \mathrm{is}\:\mathrm{1} \\ $$

Commented by Rojarani last updated on 13/May/25

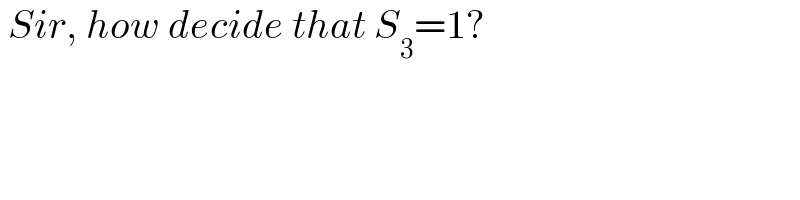
Sir, how decide that S_3 =1?

$$\:{Sir},\:{how}\:{decide}\:{that}\:{S}_{\mathrm{3}} =\mathrm{1}? \\ $$

Answered by Ghisom last updated on 13/May/25

a, b, c are the solutions of (1) x^3 −x^2 =0 ⇒ a^4 +b^4 +c^4 =1 (2) x^3 −x^2 +(1/2)=0 ⇒ a^4 +b^4 +c^4 =−1 (3) x^3 −x^2 +2=0 ⇒ a^4 +b^4 +c^4 =−7 [x^3 −x^2 +α=0 ⇒ a^4 +b^4 +c^4 =1−4α]

$${a},\:{b},\:{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =−\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}=\mathrm{0}\:\Rightarrow\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =−\mathrm{7} \\ $$$$ \\ $$$$\left[{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\alpha=\mathrm{0}\:\Rightarrow\:{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} =\mathrm{1}−\mathrm{4}\alpha\right] \\ $$

Commented by Rojarani last updated on 14/May/25

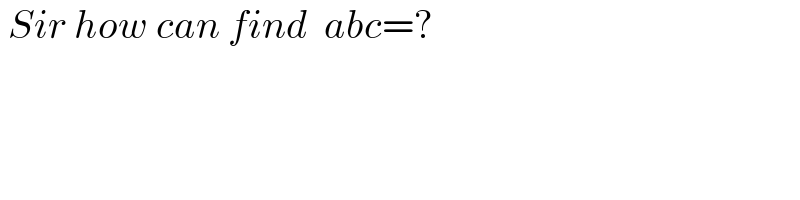
Sir how can find abc=?

$$\:{Sir}\:{how}\:{can}\:{find}\:\:{abc}=? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com