Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 187076 by Humble last updated on 13/Feb/23

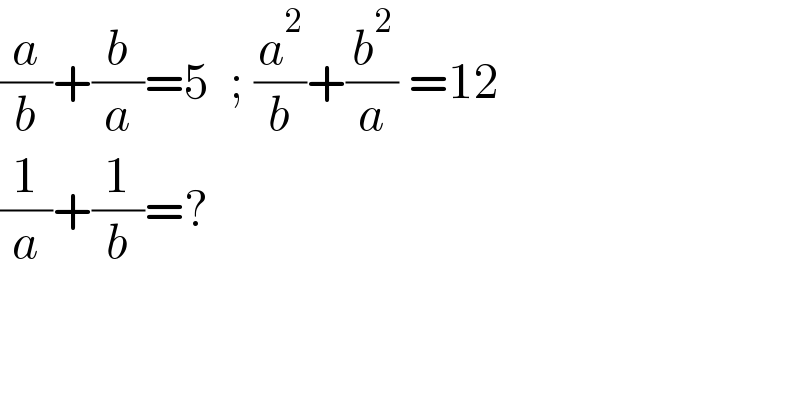
(a/b)+(b/a)=5 ; (a^2 /b)+(b^2 /a) =12 (1/a)+(1/b)=?

$$\frac{{a}}{{b}}+\frac{{b}}{{a}}=\mathrm{5}\:\:;\:\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{a}}\:=\mathrm{12} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=? \\ $$

Answered by Rasheed.Sindhi last updated on 13/Feb/23

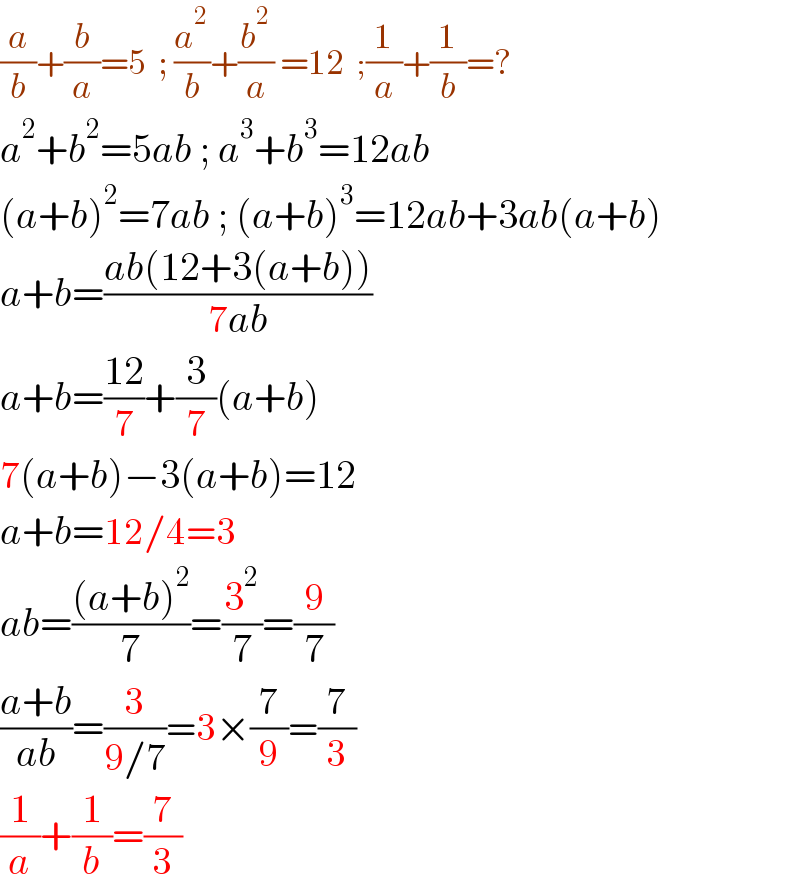
(a/b)+(b/a)=5 ; (a^2 /b)+(b^2 /a) =12 ;(1/a)+(1/b)=? a^2 +b^2 =5ab ; a^3 +b^3 =12ab (a+b)^2 =7ab ; (a+b)^3 =12ab+3ab(a+b) a+b=((ab(12+3(a+b)))/(7ab)) a+b=((12)/7)+(3/7)(a+b) 7(a+b)−3(a+b)=12 a+b=12/4=3 ab=(((a+b)^2 )/7)=(3^2 /7)=(9/7) ((a+b)/(ab))=(3/(9/7))=3×(7/9)=(7/3) (1/a)+(1/b)=(7/3)

$$\frac{{a}}{{b}}+\frac{{b}}{{a}}=\mathrm{5}\:\:;\:\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{a}}\:=\mathrm{12}\:\:;\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=? \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5}{ab}\:;\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{12}{ab} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{7}{ab}\:;\:\left({a}+{b}\right)^{\mathrm{3}} =\mathrm{12}{ab}+\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$${a}+{b}=\frac{{ab}\left(\mathrm{12}+\mathrm{3}\left({a}+{b}\right)\right)}{\mathrm{7}{ab}} \\ $$$${a}+{b}=\frac{\mathrm{12}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{7}}\left({a}+{b}\right) \\ $$$$\mathrm{7}\left({a}+{b}\right)−\mathrm{3}\left({a}+{b}\right)=\mathrm{12} \\ $$$${a}+{b}=\mathrm{12}/\mathrm{4}=\mathrm{3} \\ $$$${ab}=\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{9}}{\mathrm{7}} \\ $$$$\frac{{a}+{b}}{{ab}}=\frac{\mathrm{3}}{\mathrm{9}/\mathrm{7}}=\mathrm{3}×\frac{\mathrm{7}}{\mathrm{9}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$

Commented by BaliramKumar last updated on 13/Feb/23

step3 devid will be 7ab

$${step}\mathrm{3} \\ $$$${devid}\:{will}\:{be}\:\mathrm{7}{ab} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Feb/23

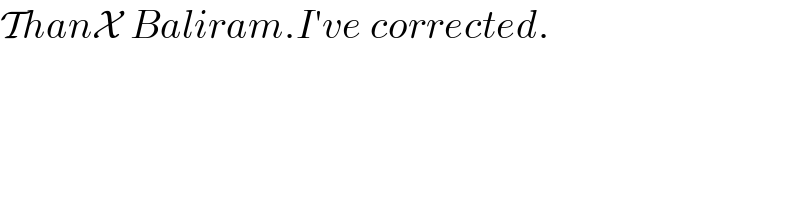
ThanX Baliram.I′ve corrected.

$$\mathcal{T}{han}\mathcal{X}\:{Baliram}.{I}'{ve}\:{corrected}. \\ $$

Commented by Humble last updated on 13/Feb/23

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by HeferH last updated on 13/Feb/23

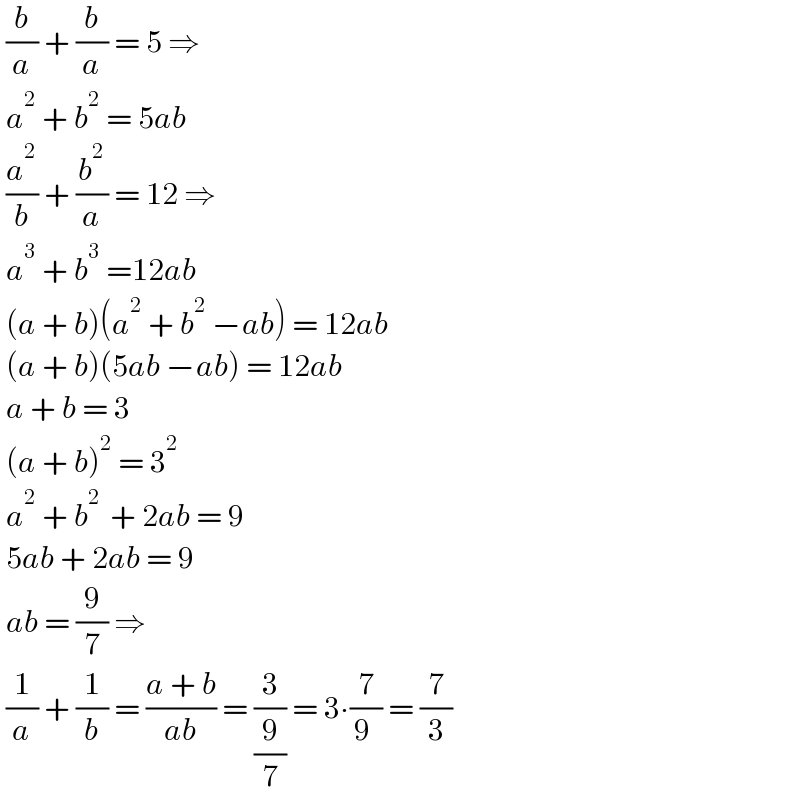
(b/a) + (b/a) = 5 ⇒ a^2 + b^2 = 5ab (a^2 /b) + (b^2 /a) = 12 ⇒ a^3 + b^3 =12ab (a + b)(a^2 + b^2 −ab) = 12ab (a + b)(5ab −ab) = 12ab a + b = 3 (a + b)^2 = 3^2 a^2 + b^(2 ) + 2ab = 9 5ab + 2ab = 9 ab = (9/7) ⇒ (1/a) + (1/b) = ((a + b)/(ab)) = (3/(9/7)) = 3∙(7/(9 )) = (7/3)

$$\:\frac{{b}}{{a}}\:+\:\frac{{b}}{{a}}\:=\:\mathrm{5}\:\Rightarrow \\ $$$$\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:=\:\mathrm{5}{ab} \\ $$$$\:\frac{{a}^{\mathrm{2}} }{{b}}\:+\:\frac{{b}^{\mathrm{2}} }{{a}}\:=\:\mathrm{12}\:\Rightarrow \\ $$$$\:{a}^{\mathrm{3}} \:+\:{b}^{\mathrm{3}} \:=\mathrm{12}{ab} \\ $$$$\:\left({a}\:+\:{b}\right)\left({a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:−{ab}\right)\:=\:\mathrm{12}{ab} \\ $$$$\:\left({a}\:+\:{b}\right)\left(\mathrm{5}{ab}\:−{ab}\right)\:=\:\mathrm{12}{ab} \\ $$$$\:{a}\:+\:{b}\:=\:\mathrm{3} \\ $$$$\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}\:} \:+\:\mathrm{2}{ab}\:=\:\mathrm{9} \\ $$$$\:\mathrm{5}{ab}\:+\:\mathrm{2}{ab}\:=\:\mathrm{9}\: \\ $$$$\:{ab}\:=\:\frac{\mathrm{9}}{\mathrm{7}}\:\Rightarrow \\ $$$$\:\frac{\mathrm{1}}{{a}}\:+\:\frac{\mathrm{1}}{{b}}\:=\:\frac{{a}\:+\:{b}}{{ab}}\:=\:\frac{\mathrm{3}}{\frac{\mathrm{9}}{\mathrm{7}}}\:=\:\mathrm{3}\centerdot\frac{\mathrm{7}}{\mathrm{9}\:}\:=\:\frac{\mathrm{7}}{\mathrm{3}} \\ $$

Commented by Humble last updated on 13/Feb/23

thank you, sir

$${thank}\:{you},\:{sir} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Feb/23

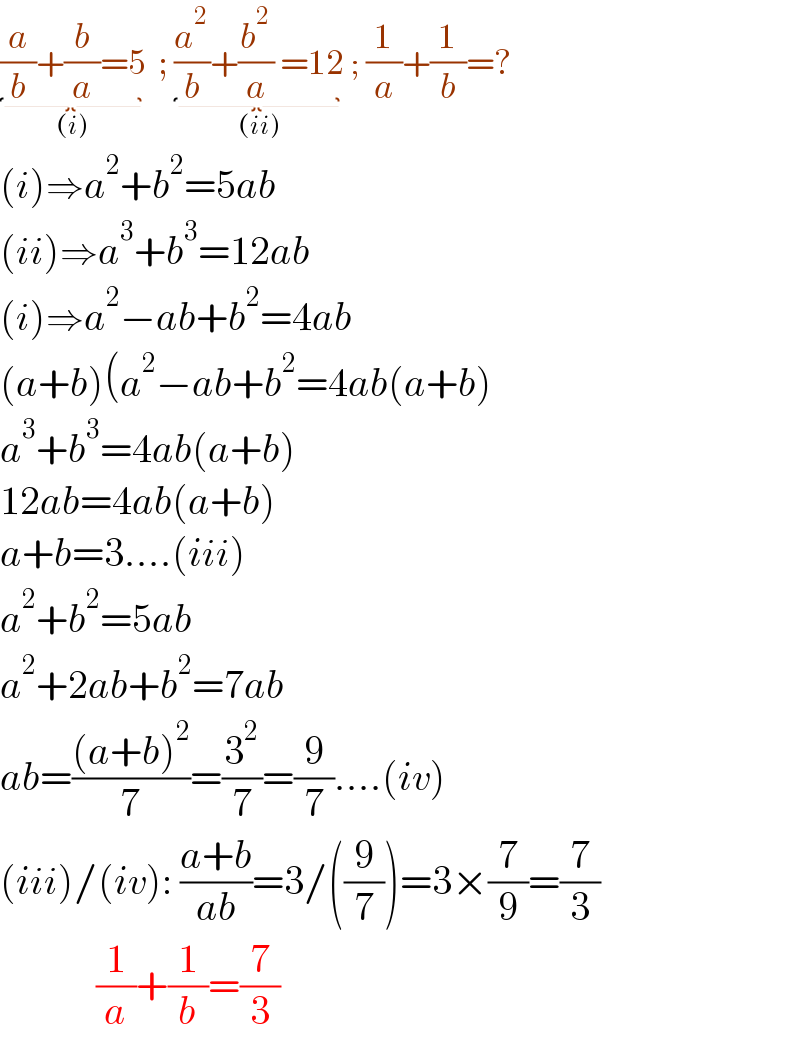
(a/b)+(b/a)=5_((i)) ; (a^2 /b)+(b^2 /a) =12_((ii)) ; (1/a)+(1/b)=? (i)⇒a^2 +b^2 =5ab (ii)⇒a^3 +b^3 =12ab (i)⇒a^2 −ab+b^2 =4ab (a+b)(a^2 −ab+b^2 =4ab(a+b) a^3 +b^3 =4ab(a+b) 12ab=4ab(a+b) a+b=3....(iii) a^2 +b^2 =5ab a^2 +2ab+b^2 =7ab ab=(((a+b)^2 )/7)=(3^2 /7)=(9/7)....(iv) (iii)/(iv): ((a+b)/(ab))=3/((9/7))=3×(7/9)=(7/3) (1/a)+(1/b)=(7/3)

$$\underset{\left({i}\right)} {\underbrace{\frac{{a}}{{b}}+\frac{{b}}{{a}}=\mathrm{5}}}\:\:;\:\underset{\left({ii}\right)} {\underbrace{\frac{{a}^{\mathrm{2}} }{{b}}+\frac{{b}^{\mathrm{2}} }{{a}}\:=\mathrm{12}}}\:;\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=? \\ $$$$\left({i}\right)\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5}{ab}\: \\ $$$$\left({ii}\right)\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{12}{ab} \\ $$$$\left({i}\right)\Rightarrow{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} =\mathrm{4}{ab} \\ $$$$\left({a}+{b}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} =\mathrm{4}{ab}\left({a}+{b}\right)\right. \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{4}{ab}\left({a}+{b}\right) \\ $$$$\mathrm{12}{ab}=\mathrm{4}{ab}\left({a}+{b}\right) \\ $$$${a}+{b}=\mathrm{3}....\left({iii}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5}{ab} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} =\mathrm{7}{ab} \\ $$$${ab}=\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{9}}{\mathrm{7}}....\left({iv}\right) \\ $$$$\left({iii}\right)/\left({iv}\right):\:\frac{{a}+{b}}{{ab}}=\mathrm{3}/\left(\frac{\mathrm{9}}{\mathrm{7}}\right)=\mathrm{3}×\frac{\mathrm{7}}{\mathrm{9}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$

Commented by Humble last updated on 14/Feb/23

thank you, sir

$${thank}\:{you},\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com