
Question Number 207436 by CrispyXYZ last updated on 15/May/24
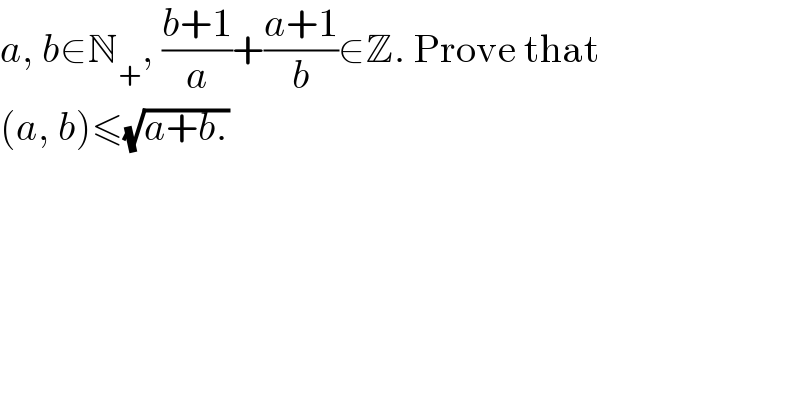
$${a},\:{b}\in\mathbb{N}_{+} ,\:\frac{{b}+\mathrm{1}}{{a}}+\frac{{a}+\mathrm{1}}{{b}}\in\mathbb{Z}.\:\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\left({a},\:{b}\right)\leqslant\sqrt{{a}+{b}.} \\ $$
Commented by A5T last updated on 15/May/24
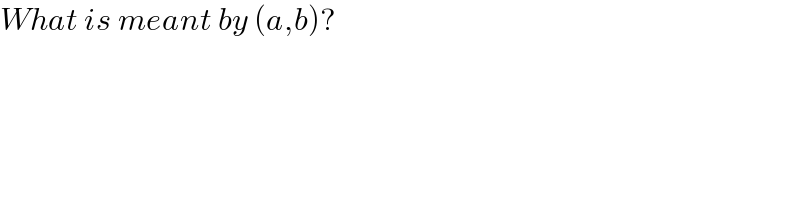
$${What}\:{is}\:{meant}\:{by}\:\left({a},{b}\right)? \\ $$
Commented by CrispyXYZ last updated on 15/May/24
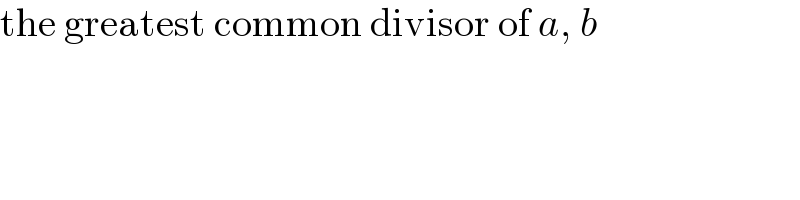
$$\mathrm{the}\:\mathrm{greatest}\:\mathrm{common}\:\mathrm{divisor}\:\mathrm{of}\:{a},\:{b} \\ $$
Answered by Berbere last updated on 16/May/24
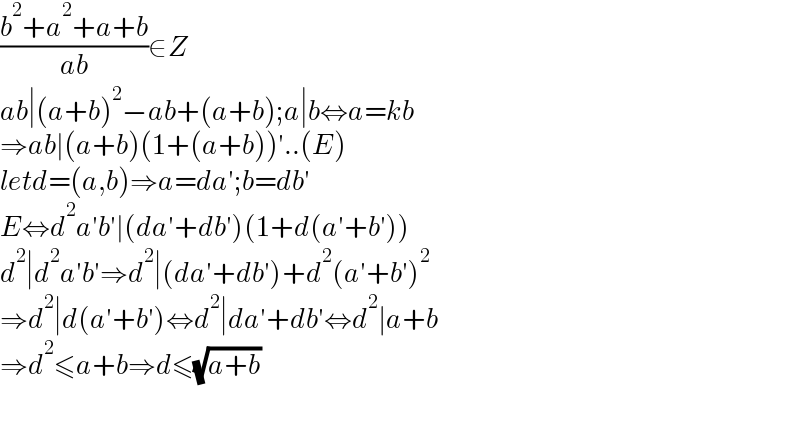
$$\frac{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} +{a}+{b}}{{ab}}\in{Z} \\ $$$${ab}\mid\left({a}+{b}\right)^{\mathrm{2}} −{ab}+\left({a}+{b}\right);{a}\mid{b}\Leftrightarrow{a}={kb} \\ $$$$\Rightarrow{ab}\mid\left({a}+{b}\right)\left(\mathrm{1}+\left({a}+{b}\right)\right)'..\left({E}\right) \\ $$$${letd}=\left({a},{b}\right)\Rightarrow{a}={da}';{b}={db}' \\ $$$${E}\Leftrightarrow{d}^{\mathrm{2}} {a}'{b}'\mid\left({da}'+{db}'\right)\left(\mathrm{1}+{d}\left({a}'+{b}'\right)\right) \\ $$$${d}^{\mathrm{2}} \mid{d}^{\mathrm{2}} {a}'{b}'\Rightarrow{d}^{\mathrm{2}} \mid\left({da}'+{db}'\right)+{d}^{\mathrm{2}} \left({a}'+{b}'\right)^{\mathrm{2}} \\ $$$$\Rightarrow{d}^{\mathrm{2}} \mid{d}\left({a}'+{b}'\right)\Leftrightarrow{d}^{\mathrm{2}} \mid{da}'+{db}'\Leftrightarrow{d}^{\mathrm{2}} \mid{a}+{b} \\ $$$$\Rightarrow{d}^{\mathrm{2}} \leqslant{a}+{b}\Rightarrow{d}\leqslant\sqrt{{a}+{b}} \\ $$$$ \\ $$
