Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 59727 by muneshkumar last updated on 14/May/19

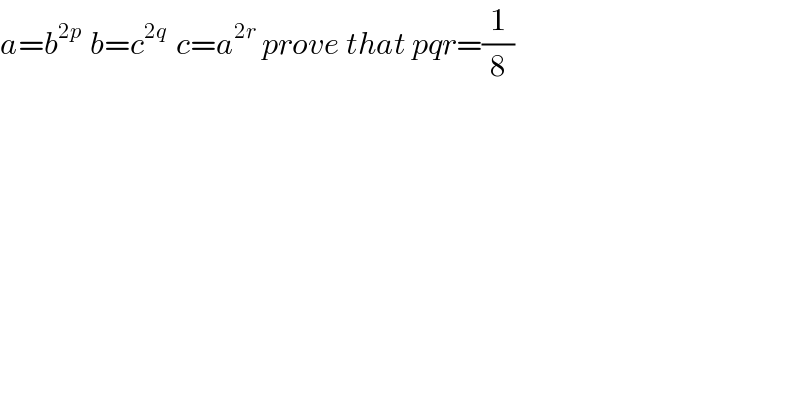
a=b^(2p ) b=c^(2q ) c=a^(2r) prove that pqr=(1/8)

$${a}={b}^{\mathrm{2}{p}\:\:} {b}={c}^{\mathrm{2}{q}\:} \:{c}={a}^{\mathrm{2}{r}} \:{prove}\:{that}\:{pqr}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Answered by MJS last updated on 13/May/19

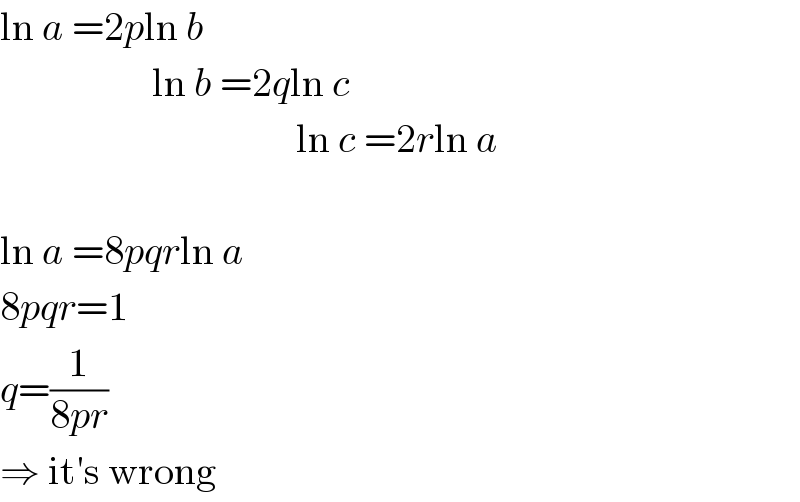
ln a =2pln b ln b =2qln c ln c =2rln a ln a =8pqrln a 8pqr=1 q=(1/(8pr)) ⇒ it′s wrong

$$\mathrm{ln}\:{a}\:=\mathrm{2}{p}\mathrm{ln}\:{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{ln}\:{b}\:=\mathrm{2}{q}\mathrm{ln}\:{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{ln}\:{c}\:=\mathrm{2}{r}\mathrm{ln}\:{a} \\ $$$$ \\ $$$$\mathrm{ln}\:{a}\:=\mathrm{8}{pqr}\mathrm{ln}\:{a} \\ $$$$\mathrm{8}{pqr}=\mathrm{1} \\ $$$${q}=\frac{\mathrm{1}}{\mathrm{8}{pr}} \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{wrong} \\ $$

Commented by $@ty@m last updated on 14/May/19

q=(1/(8pr)) ≡(1/8)=pqr what′s wrong?

$${q}=\frac{\mathrm{1}}{\mathrm{8}{pr}}\:\equiv\frac{\mathrm{1}}{\mathrm{8}}={pqr} \\ $$$${what}'{s}\:{wrong}? \\ $$

Commented by MJS last updated on 14/May/19

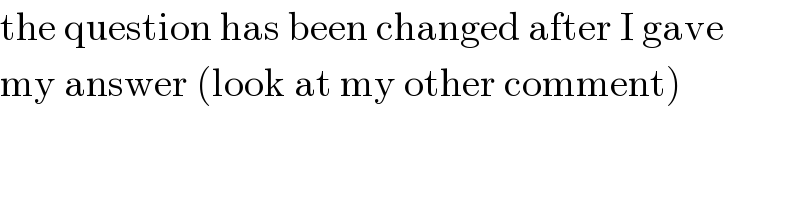
the question has been changed after I gave my answer (look at my other comment)

$$\mathrm{the}\:\mathrm{question}\:\mathrm{has}\:\mathrm{been}\:\mathrm{changed}\:\mathrm{after}\:\mathrm{I}\:\mathrm{gave} \\ $$$$\mathrm{my}\:\mathrm{answer}\:\left(\mathrm{look}\:\mathrm{at}\:\mathrm{my}\:\mathrm{other}\:\mathrm{comment}\right) \\ $$

Commented by $@ty@m last updated on 14/May/19

Oh I see. I already went through your other comment but (since the qn. has been changed) I could find its relevency.

$${Oh}\:{I}\:{see}. \\ $$$${I}\:{already}\:{went}\:{through}\:{your}\:{other} \\ $$$${comment}\:{but}\:\left({since}\:{the}\:{qn}.\:{has}\:\right. \\ $$$$\left.{been}\:{changed}\right)\:{I}\:{could}\:{find}\:{its} \\ $$$${relevency}. \\ $$

Answered by MJS last updated on 14/May/19

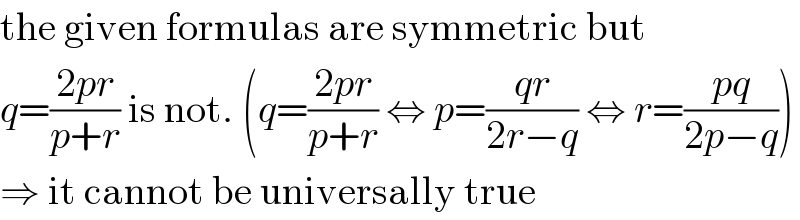
the given formulas are symmetric but q=((2pr)/(p+r)) is not. (q=((2pr)/(p+r)) ⇔ p=((qr)/(2r−q)) ⇔ r=((pq)/(2p−q))) ⇒ it cannot be universally true

$$\mathrm{the}\:\mathrm{given}\:\mathrm{formulas}\:\mathrm{are}\:\mathrm{symmetric}\:\mathrm{but} \\ $$$${q}=\frac{\mathrm{2}{pr}}{{p}+{r}}\:\mathrm{is}\:\mathrm{not}.\:\left({q}=\frac{\mathrm{2}{pr}}{{p}+{r}}\:\Leftrightarrow\:{p}=\frac{{qr}}{\mathrm{2}{r}−{q}}\:\Leftrightarrow\:{r}=\frac{{pq}}{\mathrm{2}{p}−{q}}\right) \\ $$$$\Rightarrow\:\mathrm{it}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{universally}\:\mathrm{true} \\ $$

Answered by tanmay last updated on 14/May/19

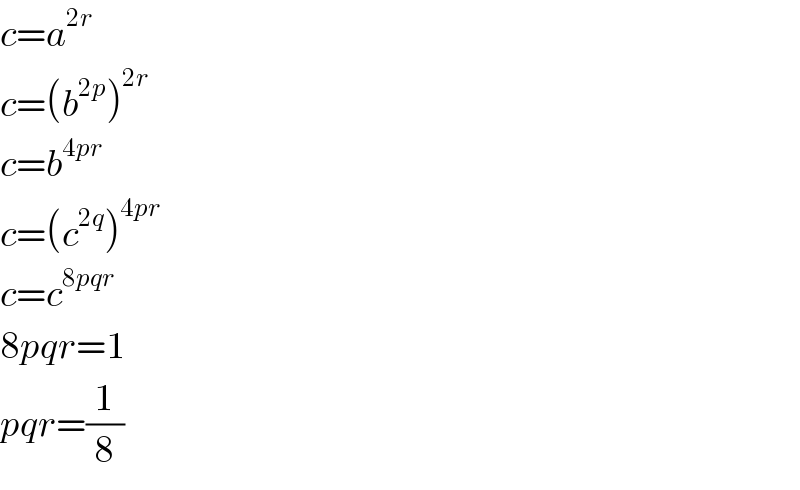
c=a^(2r) c=(b^(2p) )^(2r) c=b^(4pr) c=(c^(2q) )^(4pr) c=c^(8pqr) 8pqr=1 pqr=(1/8)

$${c}={a}^{\mathrm{2}{r}} \\ $$$${c}=\left({b}^{\mathrm{2}{p}} \right)^{\mathrm{2}{r}} \\ $$$${c}={b}^{\mathrm{4}{pr}} \\ $$$${c}=\left({c}^{\mathrm{2}{q}} \right)^{\mathrm{4}{pr}} \\ $$$${c}={c}^{\mathrm{8}{pqr}} \\ $$$$\mathrm{8}{pqr}=\mathrm{1} \\ $$$${pqr}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com