
Question Number 36132 by Rasheed.Sindhi last updated on 29/May/18

$${a}+{b}=\mathrm{10}.........\left(\mathrm{i}\right) \\ $$$${ab}+{c}=\mathrm{0}..........\left(\mathrm{ii}\right) \\ $$$${ac}+{d}=\mathrm{6}..........\left(\mathrm{iii}\right) \\ $$$${ad}=−\mathrm{1}...........\left(\mathrm{iv}\right) \\ $$$$\left({a},{b},{c},{d}\right)=? \\ $$$$\mathcal{N}{ote}:\:{This}\:{problem}\:{is}\:{related}\:{to}\:{solve} \\ $$$${the}\:{equation}\:\left({t}^{\mathrm{4}} +\mathrm{10}{t}+\mathrm{6}{t}−\mathrm{1}=\mathrm{0}\right)\:{of} \\ $$$${Q}#\mathrm{35844} \\ $$
Commented by Rasheed.Sindhi last updated on 29/May/18

$$\left(\mathrm{i}\right)\Rightarrow{a}=\mathrm{10}−{b}\Rightarrow \\ $$$$\:\:\:\left(\mathrm{ii}\right):\:\:\:\left(\mathrm{10}−{b}\right){b}+{c}=\mathrm{0}\Rightarrow{c}=\left({b}−\mathrm{10}\right){b} \\ $$$$\:\:\:\left(\mathrm{iii}\right):\:\:\left(\mathrm{10}−{b}\right){c}+{d}=\mathrm{6}\Rightarrow\left(\mathrm{10}−{b}\right)\left\{\left({b}−\mathrm{10}\right){b}\right\}=\mathrm{6} \\ $$$$\:\:\:\:\left(\mathrm{iv}\right):\left(\mathrm{10}−{b}\right){d}=−\mathrm{1} \\ $$$$\left(\mathrm{ii}\right):{c}=\left({b}−\mathrm{10}\right){b}\Rightarrow \\ $$$$\:\:\:\:\:\:\left(\mathrm{iii}\right):\left(\mathrm{10}−{b}\right)\left({b}−\mathrm{10}\right){b}−\frac{\mathrm{1}}{\mathrm{10}−{b}}=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\left({b}−\mathrm{10}\right)\left({b}−\mathrm{10}\right){b}+\frac{\mathrm{1}}{{b}−\mathrm{10}}=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:−{b}\left({b}−\mathrm{10}\right)^{\mathrm{3}} +\mathrm{1}=\mathrm{6}\left({b}−\mathrm{10}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${W}\mathrm{rongly}\:\mathrm{derived}\:\mathrm{cubic}\:\mathrm{equation}.\mathrm{Sorry}! \\ $$$${b}^{\mathrm{3}} −\mathrm{20}{b}^{\mathrm{2}} +\mathrm{100}{b}+\mathrm{6}=\mathrm{0} \\ $$$${A}\mathrm{unybody}\:\mathrm{who}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{cubic}\:\mathrm{equation}.. \\ $$
Commented by prakash jain last updated on 29/May/18

$$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{procedure}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{cubic} \\ $$$$\mathrm{equation}\:\mathrm{and}\:\mathrm{also}\:\mathrm{cubic}\:\mathrm{formula}. \\ $$$$ \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{easier}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{step}\:\mathrm{then}\:\mathrm{remembering} \\ $$$$\mathrm{the}\:\mathrm{formula}. \\ $$
Commented by mondodotto@gmail.com last updated on 29/May/18
$$\mathrm{use}\:\mathrm{a}\:\mathrm{calculator} \\ $$
Commented by prakash jain last updated on 29/May/18
http://www.sosmath.com/algebra/factor/fac11/fac11.html
Commented by Rasheed.Sindhi last updated on 29/May/18
$$\mathcal{T}{h}\infty{nk}\mathcal{S}\:\mathcal{S}{ir}!\:{I}\:{always}\:{have}\:{learnt} \\ $$$${from}\:{you}. \\ $$
Commented by MJS last updated on 29/May/18
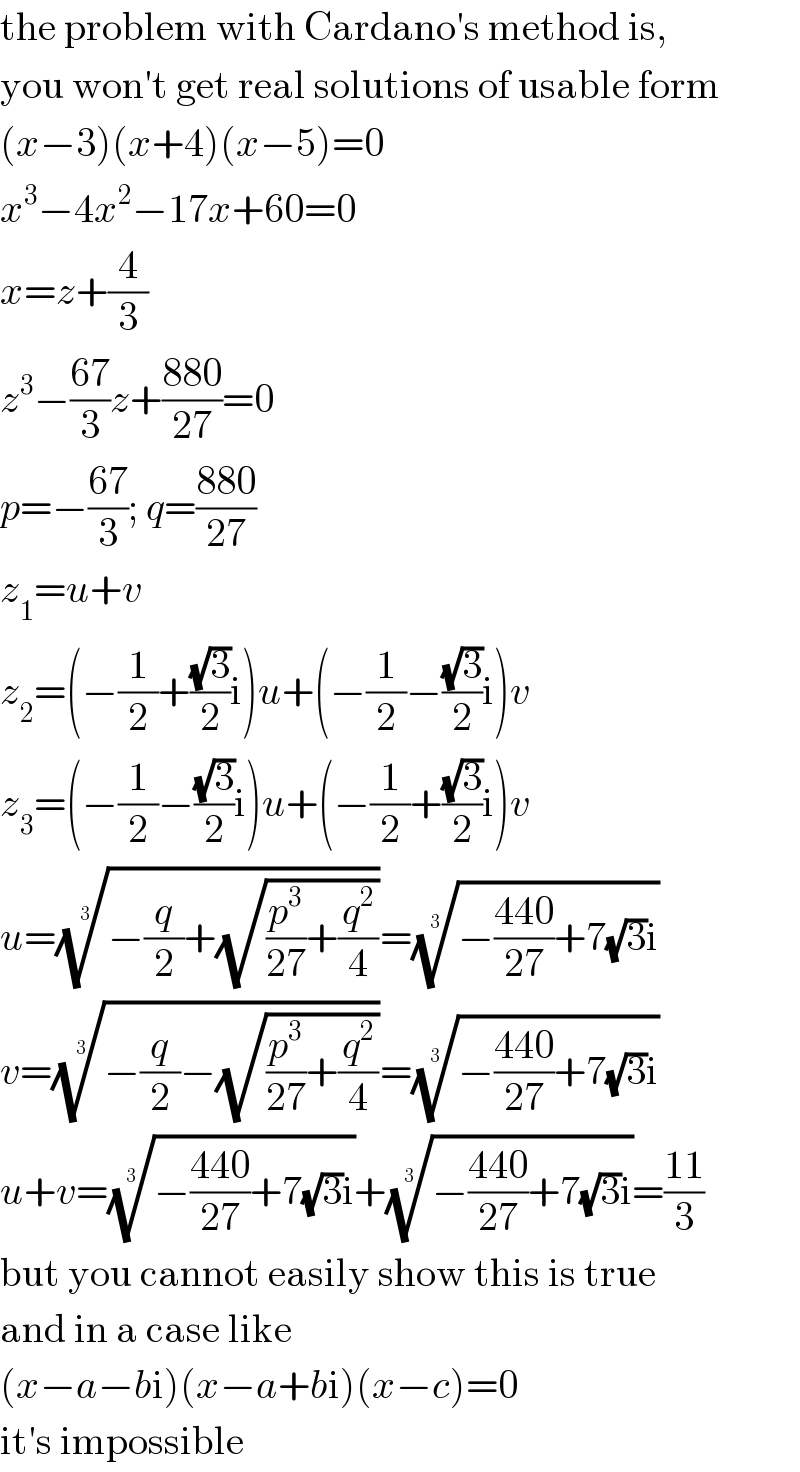
$$\mathrm{the}\:\mathrm{problem}\:\mathrm{with}\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{method}\:\mathrm{is}, \\ $$$$\mathrm{you}\:\mathrm{won}'\mathrm{t}\:\mathrm{get}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{usable}\:\mathrm{form} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}+\mathrm{4}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{17}{x}+\mathrm{60}=\mathrm{0} \\ $$$${x}={z}+\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{67}}{\mathrm{3}}{z}+\frac{\mathrm{880}}{\mathrm{27}}=\mathrm{0} \\ $$$${p}=−\frac{\mathrm{67}}{\mathrm{3}};\:{q}=\frac{\mathrm{880}}{\mathrm{27}} \\ $$$${z}_{\mathrm{1}} ={u}+{v} \\ $$$${z}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${z}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{440}}{\mathrm{27}}+\mathrm{7}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$${v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{440}}{\mathrm{27}}+\mathrm{7}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$${u}+{v}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{440}}{\mathrm{27}}+\mathrm{7}\sqrt{\mathrm{3}}\mathrm{i}}+\sqrt[{\mathrm{3}}]{−\frac{\mathrm{440}}{\mathrm{27}}+\mathrm{7}\sqrt{\mathrm{3}}\mathrm{i}}=\frac{\mathrm{11}}{\mathrm{3}} \\ $$$$\mathrm{but}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{easily}\:\mathrm{show}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true} \\ $$$$\mathrm{and}\:\mathrm{in}\:\mathrm{a}\:\mathrm{case}\:\mathrm{like} \\ $$$$\left({x}−{a}−{b}\mathrm{i}\right)\left({x}−{a}+{b}\mathrm{i}\right)\left({x}−{c}\right)=\mathrm{0} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{impossible} \\ $$
Commented by Rasheed.Sindhi last updated on 30/May/18

$$\mathcal{T}{hank}\mathcal{S}\:{a}\:{lot}\:\mathcal{S}{ir}! \\ $$
