
Question Number 119575 by mathocean1 last updated on 25/Oct/20
![a ∈ N. a is not a multiple of 3. 1) Show that a^3 ≡−1[9] or a^3 ≡1[9]. 2) Given a; b; c ∈ Z. Deduct from 1) that if a^3 +b^3 +c^3 ≡0[9] , then one of integers a; b; c is divisible by 3.](Q119575.png)
$$\mathrm{a}\:\in\:\mathbb{N}.\:\mathrm{a}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{3}. \\ $$$$\left.\mathrm{1}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{a}^{\mathrm{3}} \equiv−\mathrm{1}\left[\mathrm{9}\right]\:\mathrm{or}\:\mathrm{a}^{\mathrm{3}} \equiv\mathrm{1}\left[\mathrm{9}\right]. \\ $$$$\left.\mathrm{2}\right)\:\mathrm{Given}\:\mathrm{a};\:\mathrm{b};\:\mathrm{c}\:\in\:\mathbb{Z}. \\ $$$$\left.\mathrm{Deduct}\:\mathrm{from}\:\mathrm{1}\right)\:\mathrm{that}\:\mathrm{if}\:\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \equiv\mathrm{0}\left[\mathrm{9}\right]\:,\:\mathrm{then}\:\: \\ $$$$\mathrm{one}\:\mathrm{of}\:\mathrm{integers}\:\mathrm{a};\:\mathrm{b};\:\mathrm{c}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}. \\ $$
Answered by mindispower last updated on 25/Oct/20
![a=3k+_− 1 ⇒a^3 (3k+_− 1)^3 =27k^3 +_− 27k^2 +9k+_− 1 =9(3k^2 +_− 3k^2 +k)+_− 1 ⇒a^3 =+_− 1[9] a^3 +b^3 +c^3 ≡0[9] suppose that non of them≡0[9] ⇒a^3 ,b^3 ,c^3 ≡+_− 1[9] a^3 +b^3 +c^3 ≡(−3,−1,1,3)[9] are all possibility≠0[9] ⇒one of theme ≡0[9] exemple a=3k,b=3e+1,c=3w−1](Q119582.png)
$${a}=\mathrm{3}{k}\underset{−} {+}\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{3}} \left(\mathrm{3}{k}\underset{−} {+}\mathrm{1}\right)^{\mathrm{3}} =\mathrm{27}{k}^{\mathrm{3}} \underset{−} {+}\mathrm{27}{k}^{\mathrm{2}} +\mathrm{9}{k}\underset{−} {+}\mathrm{1} \\ $$$$=\mathrm{9}\left(\mathrm{3}{k}^{\mathrm{2}} \underset{−} {+}\mathrm{3}{k}^{\mathrm{2}} +{k}\right)\underset{−} {+}\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{3}} =\underset{−} {+}\mathrm{1}\left[\mathrm{9}\right] \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \equiv\mathrm{0}\left[\mathrm{9}\right] \\ $$$${suppose}\:{that}\:\:{non}\:{of}\:{them}\equiv\mathrm{0}\left[\mathrm{9}\right] \\ $$$$\Rightarrow{a}^{\mathrm{3}} ,{b}^{\mathrm{3}} ,{c}^{\mathrm{3}} \equiv\underset{−} {+}\mathrm{1}\left[\mathrm{9}\right] \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \equiv\left(−\mathrm{3},−\mathrm{1},\mathrm{1},\mathrm{3}\right)\left[\mathrm{9}\right] \\ $$$${are}\:{all}\:{possibility}\neq\mathrm{0}\left[\mathrm{9}\right] \\ $$$$\Rightarrow{one}\:{of}\:{theme}\:\equiv\mathrm{0}\left[\mathrm{9}\right] \\ $$$${exemple}\:{a}=\mathrm{3}{k},{b}=\mathrm{3}{e}+\mathrm{1},{c}=\mathrm{3}{w}−\mathrm{1} \\ $$
Commented by mathocean1 last updated on 25/Oct/20

$$\mathrm{please}\:\mathrm{sir}\:\mathrm{at}\:\mathrm{the}\:\mathrm{eighth}\:\mathrm{line}\:\mathrm{can}\:\mathrm{you}\:\mathrm{detail} \\ $$$$\mathrm{how}\:−\mathrm{3};\:−\mathrm{1};\:\mathrm{1};\:\mathrm{3}\:\mathrm{appeared}\:? \\ $$
Commented by mindispower last updated on 25/Oct/20
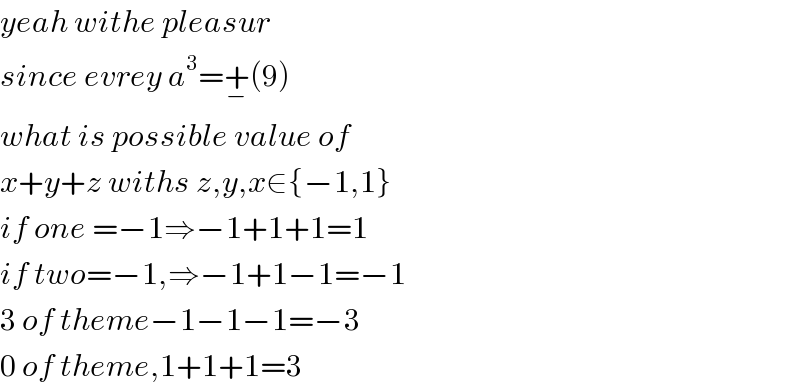
$${yeah}\:{withe}\:{pleasur}\: \\ $$$${since}\:{evrey}\:{a}^{\mathrm{3}} =\underset{−} {+}\left(\mathrm{9}\right) \\ $$$${what}\:{is}\:{possible}\:{value}\:{of} \\ $$$${x}+{y}+{z}\:{withs}\:{z},{y},{x}\in\left\{−\mathrm{1},\mathrm{1}\right\} \\ $$$${if}\:{one}\:=−\mathrm{1}\Rightarrow−\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{1} \\ $$$${if}\:{two}=−\mathrm{1},\Rightarrow−\mathrm{1}+\mathrm{1}−\mathrm{1}=−\mathrm{1} \\ $$$$\mathrm{3}\:{of}\:{theme}−\mathrm{1}−\mathrm{1}−\mathrm{1}=−\mathrm{3} \\ $$$$\mathrm{0}\:{of}\:{theme},\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{3} \\ $$
Commented by mathocean1 last updated on 25/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$
