
Question Number 114326 by 1549442205PVT last updated on 18/Sep/20

$$\left.\mathrm{a}\right)\mathrm{Find}\:\mathrm{a}\:\mathrm{four}−\mathrm{digit}\:\mathrm{number}\:\mathrm{that} \\ $$$$\mathrm{satisfies}\:\mathrm{the}\:\mathrm{following}\:\mathrm{condition}: \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{squares}\:\mathrm{of}\:\mathrm{the}\:\mathrm{extreme}\:\mathrm{digits} \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{13};\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{squares}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{middle}\:\mathrm{digits}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{85};\mathrm{if}\:\mathrm{we} \\ $$$$\mathrm{substract}\:\mathrm{1089}\:\mathrm{from}\:\mathrm{the}\:\mathrm{desired} \\ $$$$\mathrm{number}\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{a}\:\mathrm{number}\:\mathrm{containing} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{digits}\:\mathrm{as}\:\mathrm{the}\:\mathrm{desired}\:\mathrm{number} \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{reverse}\:\mathrm{order}. \\ $$$$\left.\mathrm{b}\right)\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{k}+\mathrm{m}+\mathrm{n}\:\mathrm{of}\: \\ $$$$\mathrm{three}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\: \\ $$$$\mathrm{6}\:\mathrm{then}\:\mathrm{k}^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{also}\:\:\mathrm{divisible}\:\mathrm{by6} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20
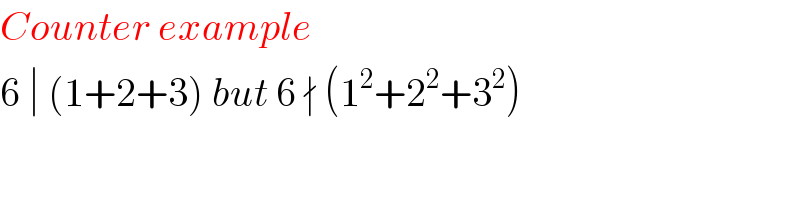
$${Counter}\:{example} \\ $$$$\mathrm{6}\:\mid\:\left(\mathrm{1}+\mathrm{2}+\mathrm{3}\right)\:{but}\:\mathrm{6}\:\nmid\:\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right) \\ $$
Commented by 1549442205PVT last updated on 18/Sep/20
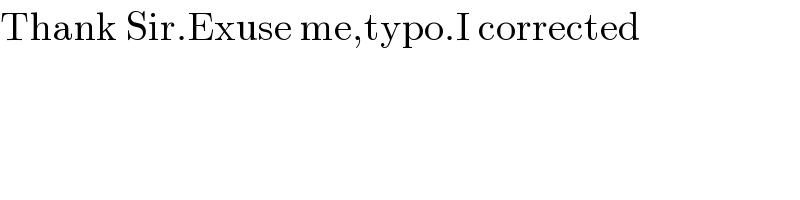
$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{Exuse}\:\mathrm{me},\mathrm{typo}.\mathrm{I}\:\mathrm{corrected} \\ $$
Answered by mr W last updated on 18/Sep/20
![[abcd] a^2 +d^2 =13 ⇒(a,d)=(2,3) or (3,2) b^2 +c^2 =85 ⇒(b,c)=(9,2) or (2,9) or (6,7) or (7,6) [abcd]−1089=[dcba] ⇒a>d ⇒a=3, d=2 [3bc2]−1089=[2cb3] 3000+100b+10c+2−1089=2000+100c+10b+3 ⇒b=c+1 ⇒b=7, c=6 ⇒the number is 3762.](Q114327.png)
$$\left[{abcd}\right] \\ $$$${a}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{13}\:\Rightarrow\left({a},{d}\right)=\left(\mathrm{2},\mathrm{3}\right)\:{or}\:\left(\mathrm{3},\mathrm{2}\right) \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{85}\:\Rightarrow\left({b},{c}\right)=\left(\mathrm{9},\mathrm{2}\right)\:{or}\:\left(\mathrm{2},\mathrm{9}\right)\:{or}\:\left(\mathrm{6},\mathrm{7}\right)\:{or}\:\left(\mathrm{7},\mathrm{6}\right) \\ $$$$\left[{abcd}\right]−\mathrm{1089}=\left[{dcba}\right] \\ $$$$\Rightarrow{a}>{d}\:\Rightarrow{a}=\mathrm{3},\:{d}=\mathrm{2} \\ $$$$\left[\mathrm{3}{bc}\mathrm{2}\right]−\mathrm{1089}=\left[\mathrm{2}{cb}\mathrm{3}\right] \\ $$$$\mathrm{3000}+\mathrm{100}{b}+\mathrm{10}{c}+\mathrm{2}−\mathrm{1089}=\mathrm{2000}+\mathrm{100}{c}+\mathrm{10}{b}+\mathrm{3} \\ $$$$\Rightarrow{b}={c}+\mathrm{1}\:\Rightarrow{b}=\mathrm{7},\:{c}=\mathrm{6} \\ $$$$\Rightarrow{the}\:{number}\:{is}\:\mathrm{3762}. \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20

$${You}'{re}\:{faster}\:{sir}! \\ $$
Commented by mr W last updated on 18/Sep/20
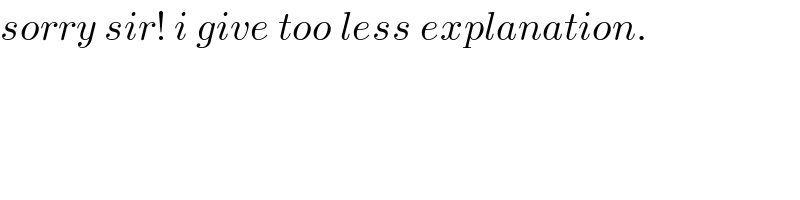
$${sorry}\:{sir}!\:{i}\:{give}\:{too}\:{less}\:{explanation}. \\ $$
Commented by mr W last updated on 18/Sep/20
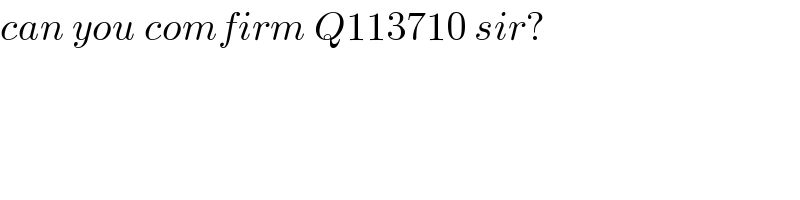
$${can}\:{you}\:{comfirm}\:{Q}\mathrm{113710}\:{sir}? \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20

$${Sorry}\:{sir}\:{I}\:{can}'{t}. \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/20
$${I}\:{think}\:{your}\:{answer}\:{is}\:{more} \\ $$$${algebraic}-{based}.{Whereas}\:{my} \\ $$$${answer}\:{somewhat}\:{more}\:{depends}\:{on} \\ $$$${trial}.{So}\:{I}\:{like}\:{yours}! \\ $$
Commented by mr W last updated on 18/Sep/20

$${thanks}\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 18/Sep/20

$${Reauired}\:{number}:\:{abcd} \\ $$$${a}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{13}.......\left({i}\right) \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{85}.........\left({ii}\right) \\ $$$${abcd}−\mathrm{1089}={dcba}.....\left({iii}\right) \\ $$$${dcba}<{abcd}\Rightarrow{d}<{a} \\ $$$${a}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{13}\:\wedge\:{d}<{a}\Rightarrow{a}^{\mathrm{2}} =\mathrm{9}\wedge{d}^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow{a}=\mathrm{3}\:\wedge\:{d}=\mathrm{2} \\ $$$${The}\:{number}\:{is}\:{now}\:\mathrm{3}{bc}\mathrm{2} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{85} \\ $$$$\mathrm{85}\:{is}\:{the}\:{sum}\:{of}\:\mathrm{81}\:{and}\:\mathrm{4}\:\left({square}\right. \\ $$$${or}\:\mathrm{36}\:{and}\:\mathrm{49}\:\left(\left({square}\:{numbers}\right)\right. \\ $$$${So}\:\left\{{b},{c}\right\}=\left\{\mathrm{2},\mathrm{9}\right\}\:{or}\:\left\{\mathrm{6},\mathrm{7}\right\} \\ $$$${The}\:{number}\:{may}\:{be} \\ $$$$\mathrm{3922}\:{or}\:\mathrm{3292}\:{or}\:\mathrm{3672}\:{or}\:\mathrm{3762} \\ $$$${Applying}\:{condition}\left({iii}\right) \\ $$$${The}\:{number}\:{is}\:\mathrm{3762} \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 18/Sep/20

$$\mathrm{6}\mid\left({k}+{m}+{n}\right) \\ $$$${k}+{m}+{n}=\mathrm{6}{x} \\ $$$${k}=\mathrm{6}{x}−{m}−{n} \\ $$$${k}^{\mathrm{3}} +{m}^{\mathrm{3}} +{n}^{\mathrm{3}} = \\ $$$$=\mathrm{18}{x}\left(\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}\left({m}+{n}\right){x}+\left({m}+{n}\right)^{\mathrm{2}} \right)−\mathrm{3}{mn}\left({m}+{n}\right) \\ $$$$\mathrm{6}\mid\left(\mathrm{18}{x}\left(\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}\left({m}+{n}\right){x}+\left({m}+{n}\right)^{\mathrm{2}} \right)\right) \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{show}\:\mathrm{6}\mid\left(\mathrm{3}{mn}\left({m}+{n}\right)\right) \\ $$$$\Leftrightarrow\:\mathrm{2}\mid{mn}\left({m}+{n}\right) \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true}\:\mathrm{if}\:\mathrm{2}\mid{m}\:\vee\:\mathrm{2}\mid{n} \\ $$$$\mathrm{and}\:\mathrm{if}\:\mathrm{both}\:{m},\:{n}\:\mathrm{are}\:\mathrm{uneven}\:\mathrm{2}\mid\left({m}+{n}\right) \\ $$$$\Rightarrow\:\mathrm{proved} \\ $$
Answered by 1549442205PVT last updated on 20/Sep/20

$$\mathrm{Thank}\:\mathrm{all}\:\mathrm{Sirs} \\ $$$$\left.\mathrm{a}\right)\mathrm{Denote}\:\mathrm{the}\:\mathrm{number}\:\mathrm{we}\:\mathrm{need}\:\mathrm{find}\:\mathrm{by} \\ $$$$\overline {\mathrm{mnpq}}.\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{m}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{13}=\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \Rightarrow\overline {\mathrm{mq}}\in\left\{\mathrm{32},\mathrm{23}\right\} \\ $$$$\mathrm{n}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{85}=\mathrm{9}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \Rightarrow\overline {\mathrm{np}}\in\left\{\mathrm{92},\mathrm{29},\mathrm{76},\mathrm{67}\right\} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{condition}\:\overline {\mathrm{mnpq}}−\mathrm{1089}=\overline {\mathrm{qpnm}} \\ $$$$\Leftrightarrow\overline {\mathrm{mnpq}}−\overline {\mathrm{qpnm}}=\mathrm{1089}\Rightarrow\mathrm{m}=\mathrm{3},\mathrm{q}=\mathrm{2} \\ $$$$\mathrm{we}\:\mathrm{hav}\:\overline {\mathrm{mnpq}}\in\left\{\mathrm{3922},\mathrm{3292},\mathrm{3762},\mathrm{3672}\right\} \\ $$$$\mathrm{Hence},\overline {\mathrm{3np2}}−\overline {\mathrm{2pn3}}=\mathrm{1089}.\mathrm{This}\:\mathrm{gives} \\ $$$$\mathrm{us}\:\overline {\mathrm{np}}=\mathrm{76}\Rightarrow\overline {\mathrm{mnpq}}=\mathrm{3762} \\ $$$$\left.\mathrm{b}\right)\mathrm{Applying}\:\mathrm{the}\:\mathrm{identity} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} −\mathrm{3abc}=\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{ab}−\mathrm{bc}−\mathrm{ca}\right) \\ $$$$\mathrm{we}\:\mathrm{have}: \\ $$$$\mathrm{k}^{\mathrm{3}} +\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} =\mathrm{3mnk}+\left(\mathrm{k}+\mathrm{m}+\mathrm{n}\right)\left(\mathrm{k}^{\mathrm{2}} +\mathrm{m}^{\mathrm{2}} \right. \\ $$$$\left.+\mathrm{n}^{\mathrm{2}} −\mathrm{km}−\mathrm{kn}−\mathrm{mn}\right) \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{m}+\mathrm{n}+\mathrm{k}\vdots\mathrm{6} \\ $$$$\Rightarrow\mathrm{m}+\mathrm{n}+\mathrm{k}=\mathrm{6p}\left(\mathrm{p}\in\mathrm{Z}\right)\Rightarrow\mathrm{among}\:\mathrm{three} \\ $$$$\mathrm{numbers}\:\mathrm{m},\mathrm{n},\mathrm{k}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{number} \\ $$$$\mathrm{is}\:\mathrm{even}\:\left(\mathrm{since}\:\:\mathrm{if}\:\mathrm{all}\:\mathrm{three}\:\mathrm{numbers}\right. \\ $$$$\mathrm{are}\:\mathrm{odd}\:\mathrm{then}\:\mathrm{m}+\mathrm{n}+\mathrm{k}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{then} \\ $$$$\mathrm{m}+\mathrm{n}+\mathrm{k}\:\mathrm{isn}'\mathrm{t}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2},\mathrm{so}\:\mathrm{isn}'\mathrm{t} \\ $$$$\left.\mathrm{divisible}\:\mathrm{by}\:\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{3mnk}\vdots\mathrm{6},\mathrm{but}\:\mathrm{m}+\mathrm{n}+\mathrm{k}\vdots\mathrm{6} \\ $$$$\Rightarrow\mathrm{m}^{\mathrm{3}} +\mathrm{n}^{\mathrm{3}} +\mathrm{k}^{\mathrm{3}} \vdots\mathrm{6}\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$
