
Question Number 194991 by York12 last updated on 21/Jul/23
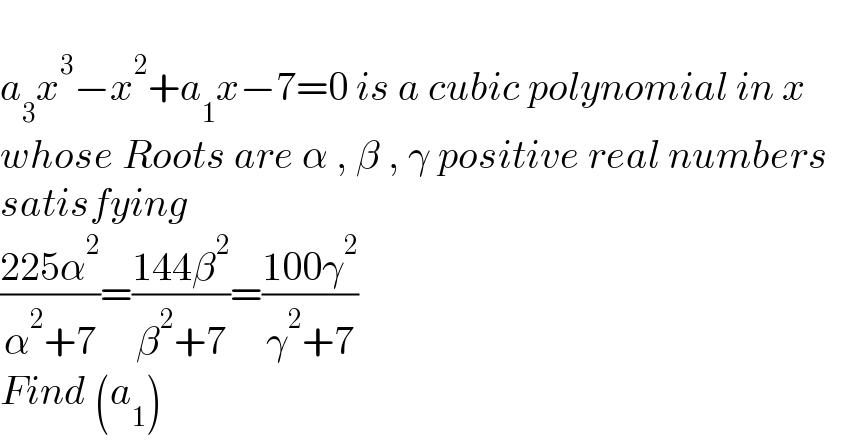
$$ \\ $$$${a}_{\mathrm{3}} {x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{a}_{\mathrm{1}} {x}−\mathrm{7}=\mathrm{0}\:{is}\:{a}\:{cubic}\:{polynomial}\:{in}\:{x} \\ $$$${whose}\:{Roots}\:{are}\:\alpha\:,\:\beta\:,\:\gamma\:{positive}\:{real}\:{numbers} \\ $$$${satisfying} \\ $$$$\frac{\mathrm{225}\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} +\mathrm{7}}=\frac{\mathrm{144}\beta^{\mathrm{2}} }{\beta^{\mathrm{2}} +\mathrm{7}}=\frac{\mathrm{100}\gamma^{\mathrm{2}} }{\gamma^{\mathrm{2}} +\mathrm{7}} \\ $$$${Find}\:\left({a}_{\mathrm{1}} \right) \\ $$
Commented by Frix last updated on 21/Jul/23
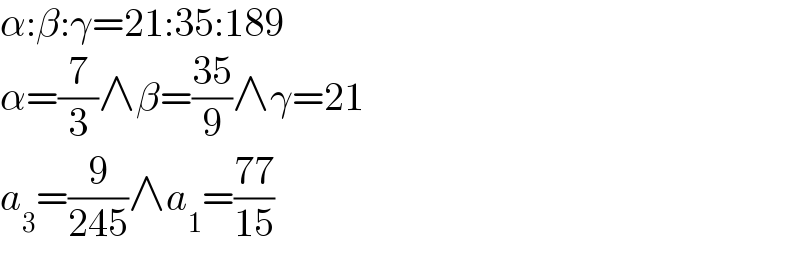
$$\alpha:\beta:\gamma=\mathrm{21}:\mathrm{35}:\mathrm{189} \\ $$$$\alpha=\frac{\mathrm{7}}{\mathrm{3}}\wedge\beta=\frac{\mathrm{35}}{\mathrm{9}}\wedge\gamma=\mathrm{21} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{245}}\wedge{a}_{\mathrm{1}} =\frac{\mathrm{77}}{\mathrm{15}} \\ $$
Commented by York12 last updated on 21/Jul/23
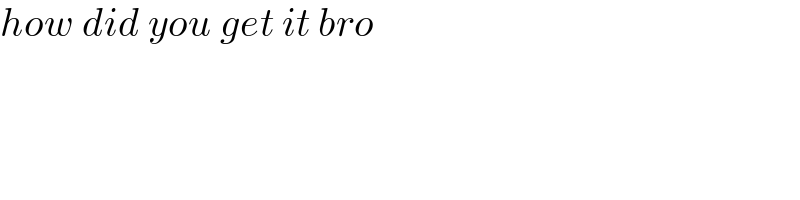
$${how}\:{did}\:{you}\:{get}\:{it}\:{bro} \\ $$
Commented by York12 last updated on 21/Jul/23

$${and}\:{what}\:{is}\:{your}\:{advice}\:{to}\:{get}\:{better}\:{at}\:{solving} \\ $$$${such}\:{problems} \\ $$$$ \\ $$
Commented by York12 last updated on 22/Jul/23
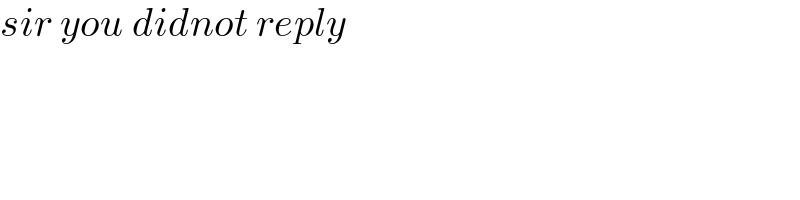
$${sir}\:{you}\:{didnot}\:{reply} \\ $$$$ \\ $$
