
Question Number 66216 by Rio Michael last updated on 11/Aug/19
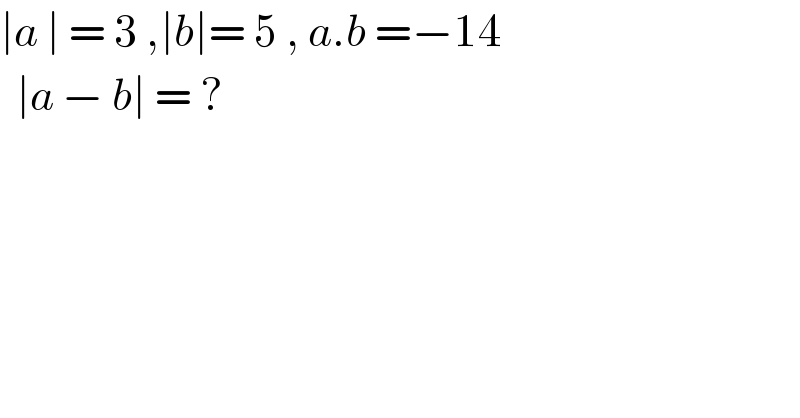
$$\mid{a}\:\mid\:=\:\mathrm{3}\:,\mid{b}\mid=\:\mathrm{5}\:,\:{a}.{b}\:=−\mathrm{14} \\ $$$$\:\:\mid{a}\:−\:{b}\mid\:=\:? \\ $$
Commented by Rasheed.Sindhi last updated on 11/Aug/19
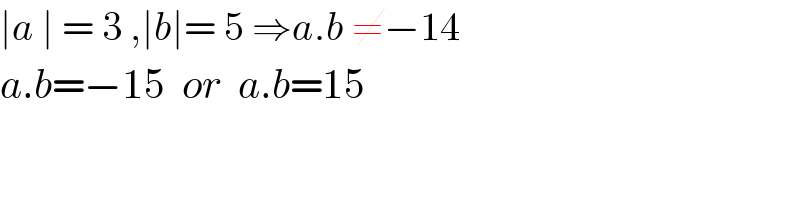
$$\mid{a}\:\mid\:=\:\mathrm{3}\:,\mid{b}\mid=\:\mathrm{5}\:\Rightarrow{a}.{b}\:\neq−\mathrm{14} \\ $$$${a}.{b}=−\mathrm{15}\:\:{or}\:\:{a}.{b}=\mathrm{15} \\ $$
Commented by behi83417@gmail.com last updated on 11/Aug/19
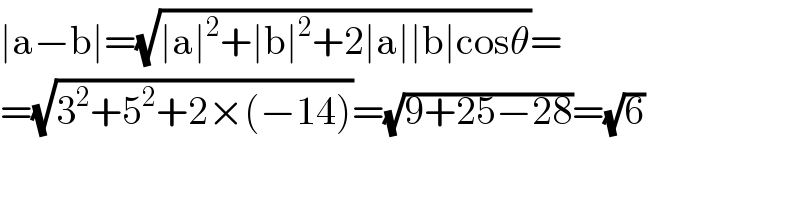
$$\mid\mathrm{a}−\mathrm{b}\mid=\sqrt{\mid\mathrm{a}\mid^{\mathrm{2}} +\mid\mathrm{b}\mid^{\mathrm{2}} +\mathrm{2}\mid\mathrm{a}\mid\mid\mathrm{b}\mid\mathrm{cos}\theta}= \\ $$$$=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{2}×\left(−\mathrm{14}\right)}=\sqrt{\mathrm{9}+\mathrm{25}−\mathrm{28}}=\sqrt{\mathrm{6}} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Aug/19
![∣a ∣ = 3 ,∣b∣= 5 , a.b =−15 ∣a − b∣ = ? ∣a∣ = 3⇒a=±3⇒b=∓5 [∵a.b=−15] ∣a − b∣=∣(±3)−(∓5)∣ =∣(±3)+(±5)∣ =∣±8∣=8](Q66219.png)
$$\mid{a}\:\mid\:=\:\mathrm{3}\:,\mid{b}\mid=\:\mathrm{5}\:,\:{a}.{b}\:=−\mathrm{15} \\ $$$$\:\:\mid{a}\:−\:{b}\mid\:=\:? \\ $$$$\:\:\mid{a}\mid\:=\:\mathrm{3}\Rightarrow{a}=\pm\mathrm{3}\Rightarrow{b}=\mp\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\because{a}.{b}=−\mathrm{15}\right] \\ $$$$\:\:\:\mid{a}\:−\:{b}\mid=\mid\left(\pm\mathrm{3}\right)−\left(\mp\mathrm{5}\right)\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\left(\pm\mathrm{3}\right)+\left(\pm\mathrm{5}\right)\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\pm\mathrm{8}\mid=\mathrm{8} \\ $$
Commented by Rio Michael last updated on 11/Aug/19

$${thanks} \\ $$
