
Question Number 122397 by Ar Brandon last updated on 16/Nov/20
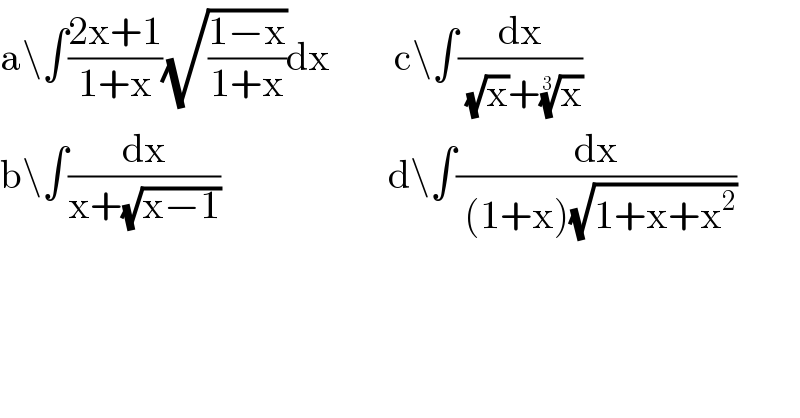
$$\mathrm{a}\backslash\int\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{1}+\mathrm{x}}\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\mathrm{dx}\:\:\:\:\:\:\:\:\mathrm{c}\backslash\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}}+\sqrt[{\mathrm{3}}]{\mathrm{x}}} \\ $$$$\mathrm{b}\backslash\int\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}−\mathrm{1}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{d}\backslash\int\frac{\mathrm{dx}}{\:\left(\mathrm{1}+\mathrm{x}\right)\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Nov/20
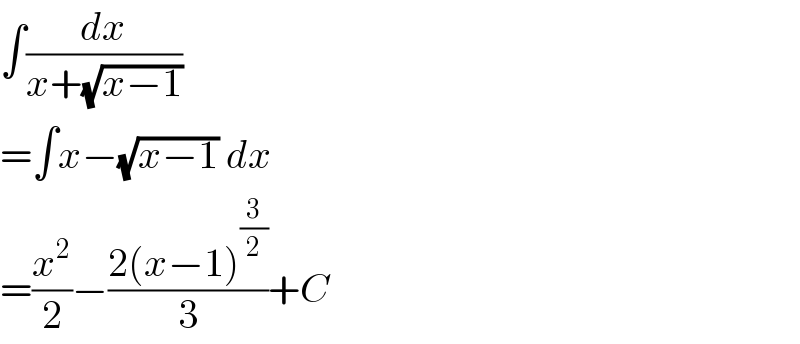
$$\int\frac{{dx}}{{x}+\sqrt{{x}−\mathrm{1}}} \\ $$$$=\int{x}−\sqrt{{x}−\mathrm{1}}\:{dx} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{2}\left({x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}+{C} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Nov/20
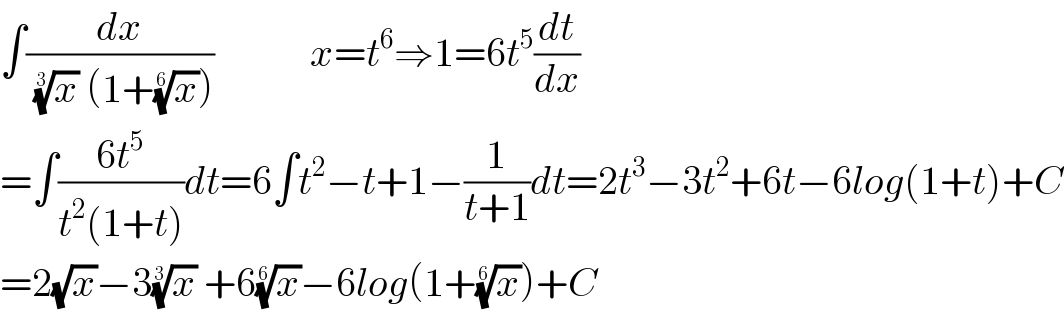
$$\int\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}\:\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}\right)}\:\:\:\:\:\:\:\:\:\:\:\:{x}={t}^{\mathrm{6}} \Rightarrow\mathrm{1}=\mathrm{6}{t}^{\mathrm{5}} \frac{{dt}}{{dx}} \\ $$$$=\int\frac{\mathrm{6}{t}^{\mathrm{5}} }{{t}^{\mathrm{2}} \left(\mathrm{1}+{t}\right)}{dt}=\mathrm{6}\int{t}^{\mathrm{2}} −{t}+\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}{dt}=\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{6}{log}\left(\mathrm{1}+{t}\right)+{C} \\ $$$$=\mathrm{2}\sqrt{{x}}−\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}\:+\mathrm{6}\sqrt[{\mathrm{6}}]{{x}}−\mathrm{6}{log}\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}\right)+{C} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Nov/20
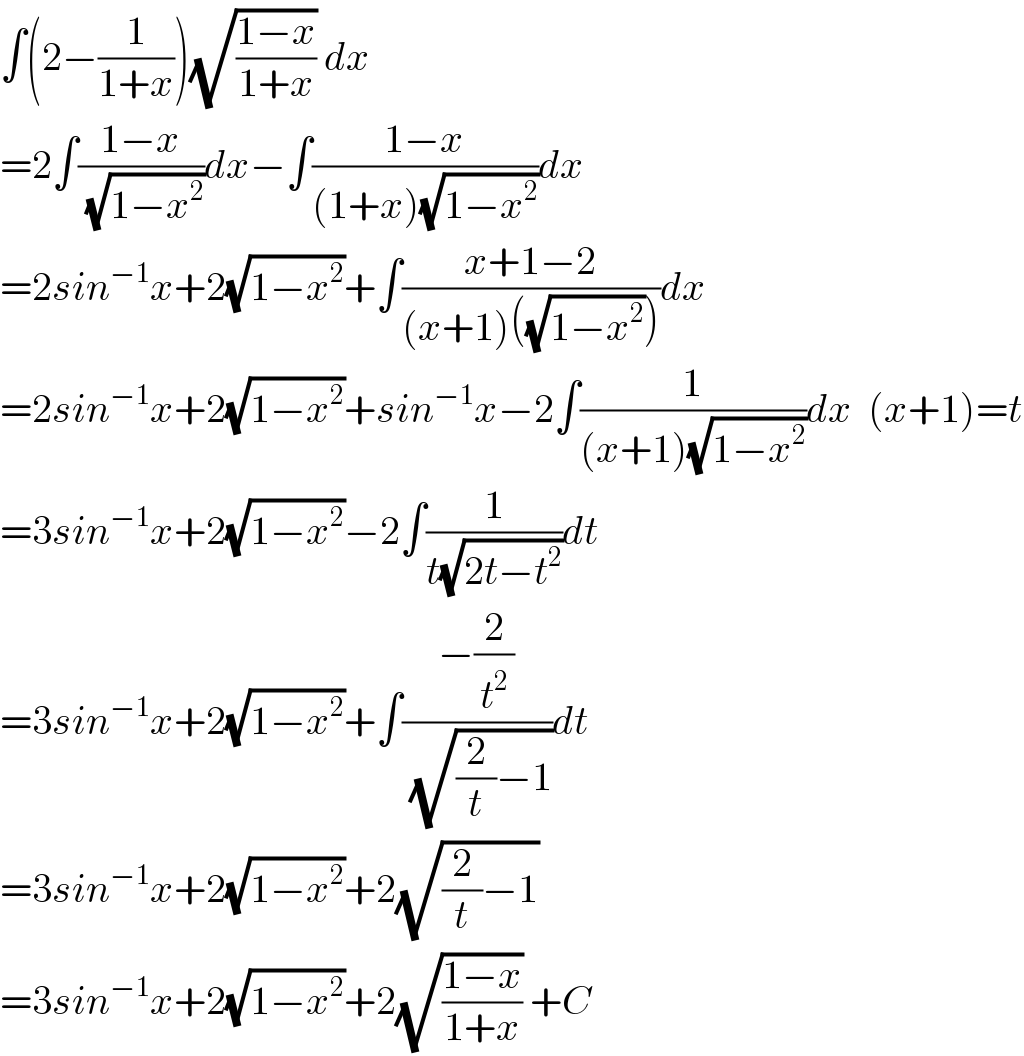
$$\int\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:{dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\int\frac{\mathrm{1}−{x}}{\left(\mathrm{1}+{x}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\int\frac{{x}+\mathrm{1}−\mathrm{2}}{\left({x}+\mathrm{1}\right)\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}{dx} \\ $$$$=\mathrm{2}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{sin}^{−\mathrm{1}} {x}−\mathrm{2}\int\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:\:\left({x}+\mathrm{1}\right)={t} \\ $$$$=\mathrm{3}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{2}\int\frac{\mathrm{1}}{{t}\sqrt{\mathrm{2}{t}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=\mathrm{3}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\int\frac{−\frac{\mathrm{2}}{{t}^{\mathrm{2}} }}{\:\sqrt{\frac{\mathrm{2}}{{t}}−\mathrm{1}}}{dt} \\ $$$$=\mathrm{3}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\frac{\mathrm{2}}{{t}}−\mathrm{1}}\: \\ $$$$=\mathrm{3}{sin}^{−\mathrm{1}} {x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{2}\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:+{C} \\ $$
Commented by Ar Brandon last updated on 16/Nov/20
Nice path. Thanks
Answered by MJS_new last updated on 17/Nov/20
![∫((2x+1)/(1+x))(√((1−x)/(1+x)))dx= [t=(√((1−x)/(1+x))) → dx=−(√(1−x))(1+x)^(3/2) dt] =2∫((t^2 (t^2 −3))/((t^2 +1)^2 ))dt= [Ostrogradski′s Method] =((2t(t^2 +3))/(t^2 +1))−6∫(dt/(t^2 +1))= =((2t(t^2 +3))/(t^2 +1))−6arctan t = =2(x+2)(√((1−x)/(1+x)))−6arctan (√((1−x)/(1+x))) +C ∫(dx/(x+(√(x−1))))= [t=(√(x−1)) → dx=2tdt] =2∫(t/(t^2 +t+1))dt=∫(((2t+1)/(t^2 +t+1))−(1/(t^2 +t+1)))dt= =ln (t^2 +t+1) −((2(√3))/3)arctan (((2t+1)(√3))/3) = =ln (x+(√(x−1))) −((2(√3))/3)arctan (((1+2(√(x−1)))(√3))/3) +C ∫(dx/( (√x)+(x)^(1/3) ))=∫(dx/(x^(1/3) (x^(1/6) +1)))= [t=x^(1/6) → dx=6x^(5/6) dt] =6∫(t^3 /(t+1))dt=6∫(t^2 −t+1−(1/(t+1)))dt= =2t^3 −3t^2 +6t−6ln (t+1) = =2x^(1/2) −3x^(1/3) +6x^(1/6) −6ln (x^(1/6) +1) +C ∫(dx/((1+x)(√(1+x+x^2 ))))= [t=((2x+1+2(√(x^2 +x+1)))/( (√3))) → dx=((√(3(x^2 +x+1)))/(2x+1+(√(x^2 +x+1))))dt] =4(√3)∫(dt/(3t^2 +2(√3)t−3))= =∫((1/(t−((√3)/3)))−(1/(t+(√3))))dt= =ln ((t−((√3)/3))/(t+(√3))) =ln ((x−1+2(√(x^2 +x+1)))/(x+1)) +C](Q122427.png)
$$\int\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{1}+{x}}\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:\rightarrow\:{dx}=−\sqrt{\mathrm{1}−{x}}\left(\mathrm{1}+{x}\right)^{\mathrm{3}/\mathrm{2}} {dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}−\mathrm{6}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}−\mathrm{6arctan}\:{t}\:= \\ $$$$=\mathrm{2}\left({x}+\mathrm{2}\right)\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}−\mathrm{6arctan}\:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:+{C} \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}+\sqrt{{x}−\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}−\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}{tdt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}=\int\left(\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\right){dt}= \\ $$$$=\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\left(\mathrm{2}{t}+\mathrm{1}\right)\sqrt{\mathrm{3}}}{\mathrm{3}}\:= \\ $$$$=\mathrm{ln}\:\left({x}+\sqrt{{x}−\mathrm{1}}\right)\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\left(\mathrm{1}+\mathrm{2}\sqrt{{x}−\mathrm{1}}\right)\sqrt{\mathrm{3}}}{\mathrm{3}}\:+{C} \\ $$$$ \\ $$$$\int\frac{{dx}}{\:\sqrt{{x}}+\sqrt[{\mathrm{3}}]{{x}}}=\int\frac{{dx}}{{x}^{\mathrm{1}/\mathrm{3}} \left({x}^{\mathrm{1}/\mathrm{6}} +\mathrm{1}\right)}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{1}/\mathrm{6}} \:\rightarrow\:{dx}=\mathrm{6}{x}^{\mathrm{5}/\mathrm{6}} {dt}\right] \\ $$$$=\mathrm{6}\int\frac{{t}^{\mathrm{3}} }{{t}+\mathrm{1}}{dt}=\mathrm{6}\int\left({t}^{\mathrm{2}} −{t}+\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$=\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{6ln}\:\left({t}+\mathrm{1}\right)\:= \\ $$$$=\mathrm{2}{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{3}{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{6}{x}^{\mathrm{1}/\mathrm{6}} −\mathrm{6ln}\:\left({x}^{\mathrm{1}/\mathrm{6}} +\mathrm{1}\right)\:+{C} \\ $$$$ \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}}{\mathrm{2}{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dt}\right] \\ $$$$=\mathrm{4}\sqrt{\mathrm{3}}\int\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{t}−\mathrm{3}}= \\ $$$$=\int\left(\frac{\mathrm{1}}{{t}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}−\frac{\mathrm{1}}{{t}+\sqrt{\mathrm{3}}}\right){dt}= \\ $$$$=\mathrm{ln}\:\frac{{t}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\:=\mathrm{ln}\:\frac{{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}+\mathrm{1}}\:+{C} \\ $$
