Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 203933 by liuxinnan last updated on 02/Feb/24

a^2 +b^2 +2c^2 =22 prove a+2b+c≤11

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} =\mathrm{22} \\ $$$${prove}\:{a}+\mathrm{2}{b}+{c}\leqslant\mathrm{11} \\ $$

Answered by York12 last updated on 02/Feb/24

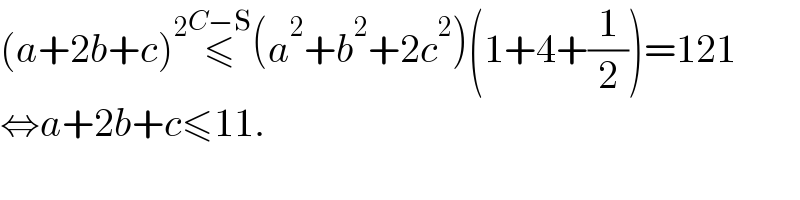
(a+2b+c)^2 ≤^(C−S) (a^2 +b^2 +2c^2 )(1+4+(1/2))=121 ⇔a+2b+c≤11.

$$\left({a}+\mathrm{2}{b}+{c}\right)^{\mathrm{2}} \overset{{C}−\mathrm{S}} {\leqslant}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{121} \\ $$$$\Leftrightarrow{a}+\mathrm{2}{b}+{c}\leqslant\mathrm{11}. \\ $$

Answered by witcher3 last updated on 02/Feb/24

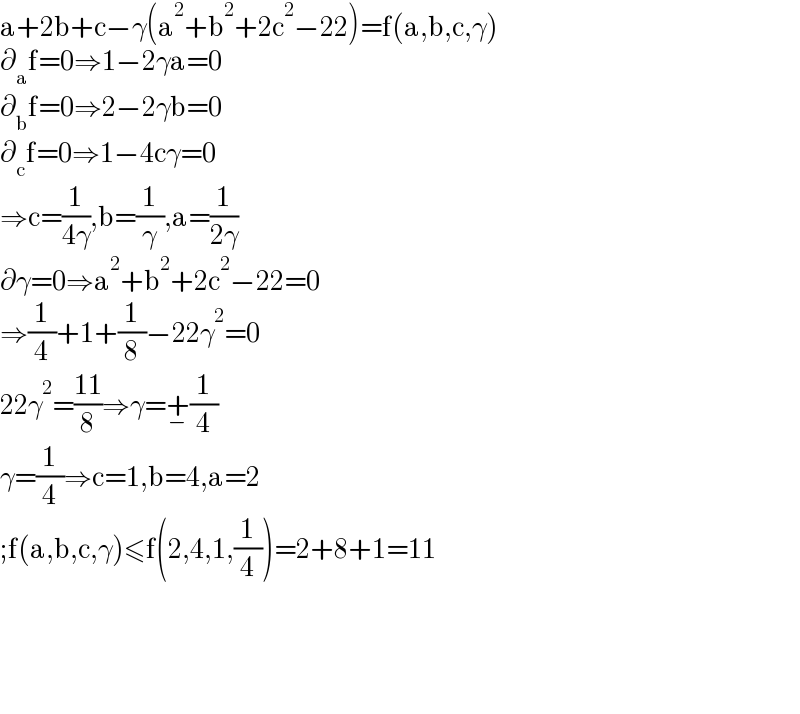
a+2b+c−γ(a^2 +b^2 +2c^2 −22)=f(a,b,c,γ) ∂_a f=0⇒1−2γa=0 ∂_b f=0⇒2−2γb=0 ∂_c f=0⇒1−4cγ=0 ⇒c=(1/(4γ)),b=(1/γ),a=(1/(2γ)) ∂γ=0⇒a^2 +b^2 +2c^2 −22=0 ⇒(1/4)+1+(1/8)−22γ^2 =0 22γ^2 =((11)/8)⇒γ=+_− (1/4) γ=(1/4)⇒c=1,b=4,a=2 ;f(a,b,c,γ)≤f(2,4,1,(1/4))=2+8+1=11

$$\mathrm{a}+\mathrm{2b}+\mathrm{c}−\gamma\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2c}^{\mathrm{2}} −\mathrm{22}\right)=\mathrm{f}\left(\mathrm{a},\mathrm{b},\mathrm{c},\gamma\right) \\ $$$$\partial_{\mathrm{a}} \mathrm{f}=\mathrm{0}\Rightarrow\mathrm{1}−\mathrm{2}\gamma\mathrm{a}=\mathrm{0} \\ $$$$\partial_{\mathrm{b}} \mathrm{f}=\mathrm{0}\Rightarrow\mathrm{2}−\mathrm{2}\gamma\mathrm{b}=\mathrm{0} \\ $$$$\partial_{\mathrm{c}} \mathrm{f}=\mathrm{0}\Rightarrow\mathrm{1}−\mathrm{4c}\gamma=\mathrm{0} \\ $$$$\Rightarrow\mathrm{c}=\frac{\mathrm{1}}{\mathrm{4}\gamma},\mathrm{b}=\frac{\mathrm{1}}{\gamma},\mathrm{a}=\frac{\mathrm{1}}{\mathrm{2}\gamma} \\ $$$$\partial\gamma=\mathrm{0}\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2c}^{\mathrm{2}} −\mathrm{22}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{22}\gamma^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{22}\gamma^{\mathrm{2}} =\frac{\mathrm{11}}{\mathrm{8}}\Rightarrow\gamma=\underset{−} {+}\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\gamma=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{c}=\mathrm{1},\mathrm{b}=\mathrm{4},\mathrm{a}=\mathrm{2} \\ $$$$;\mathrm{f}\left(\mathrm{a},\mathrm{b},\mathrm{c},\gamma\right)\leqslant\mathrm{f}\left(\mathrm{2},\mathrm{4},\mathrm{1},\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{2}+\mathrm{8}+\mathrm{1}=\mathrm{11} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by York12 last updated on 02/Feb/24

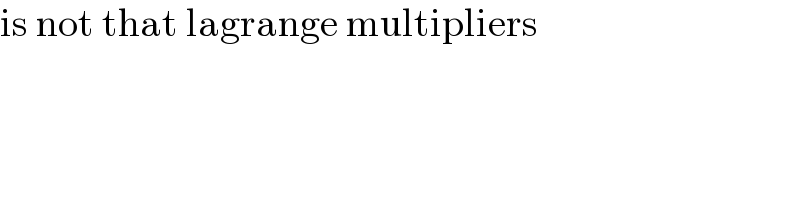
is not that lagrange multipliers

$$\mathrm{is}\:\mathrm{not}\:\mathrm{that}\:\mathrm{lagrange}\:\mathrm{multipliers} \\ $$

Commented by witcher3 last updated on 04/Feb/24

yes

$$\mathrm{yes}\: \\ $$

Commented by York12 last updated on 04/Feb/24

great

$$\mathrm{great} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com