
Question Number 113006 by Aina Samuel Temidayo last updated on 10/Sep/20
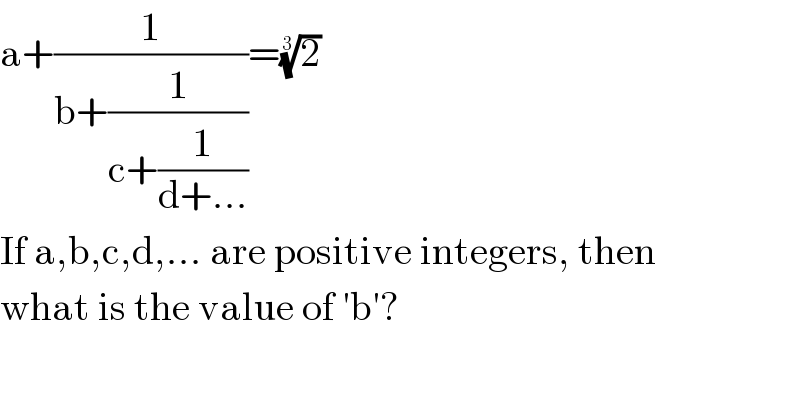
$$\mathrm{a}+\frac{\mathrm{1}}{\mathrm{b}+\frac{\mathrm{1}}{\mathrm{c}+\frac{\mathrm{1}}{\mathrm{d}+...}}}=\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},...\:\mathrm{are}\:\mathrm{positive}\:\mathrm{integers},\:\mathrm{then} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:'\mathrm{b}'? \\ $$
Answered by mr W last updated on 11/Sep/20
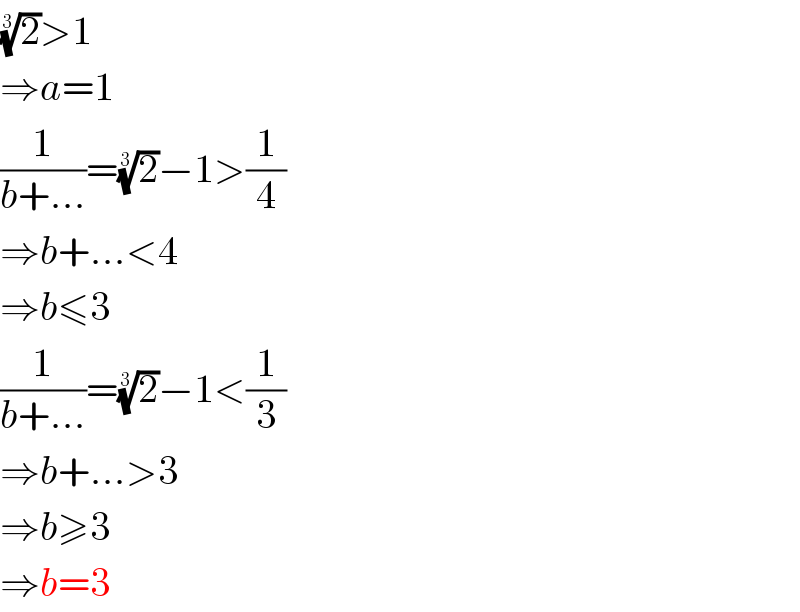
$$\sqrt[{\mathrm{3}}]{\mathrm{2}}>\mathrm{1} \\ $$$$\Rightarrow{a}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{b}+...}=\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{b}+...<\mathrm{4} \\ $$$$\Rightarrow{b}\leqslant\mathrm{3} \\ $$$$\frac{\mathrm{1}}{{b}+...}=\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}<\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{b}+...>\mathrm{3} \\ $$$$\Rightarrow{b}\geqslant\mathrm{3} \\ $$$$\Rightarrow{b}=\mathrm{3} \\ $$
Commented by Aina Samuel Temidayo last updated on 11/Sep/20

$$\mathrm{Why}\:\mathrm{is}\:\mathrm{a}=\mathrm{1}\:? \\ $$
Commented by mr W last updated on 11/Sep/20
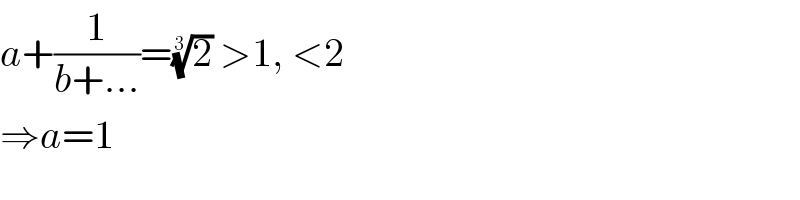
$${a}+\frac{\mathrm{1}}{{b}+...}=\sqrt[{\mathrm{3}}]{\mathrm{2}}\:>\mathrm{1},\:<\mathrm{2} \\ $$$$\Rightarrow{a}=\mathrm{1} \\ $$
