
Question Number 193199 by mnjuly1970 last updated on 07/Jun/23
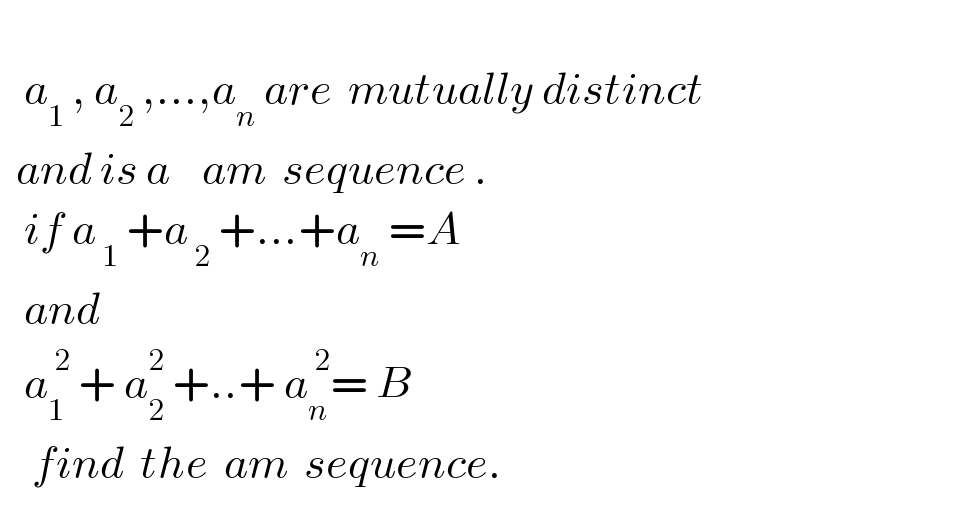
$$ \\ $$$$\:\:\:{a}_{\mathrm{1}} \:,\:{a}_{\mathrm{2}} \:,...,{a}_{{n}} \:{are}\:\:{mutually}\:{distinct} \\ $$$$\:\:{and}\:{is}\:{a}\:\:\:\:{am}\:\:{sequence}\:. \\ $$$$\:\:\:{if}\:{a}_{\:\mathrm{1}} \:+{a}_{\:\mathrm{2}} \:+...+{a}_{{n}} \:={A} \\ $$$$\:\:\:{and}\:\: \\ $$$$\:\:\:{a}_{\mathrm{1}} ^{\:\mathrm{2}} \:+\:{a}_{\mathrm{2}} ^{\mathrm{2}} \:+..+\:{a}_{{n}} ^{\:\mathrm{2}} =\:{B} \\ $$$$\:\:\:\:{find}\:\:{the}\:\:{am}\:\:{sequence}. \\ $$
Answered by MM42 last updated on 07/Jun/23
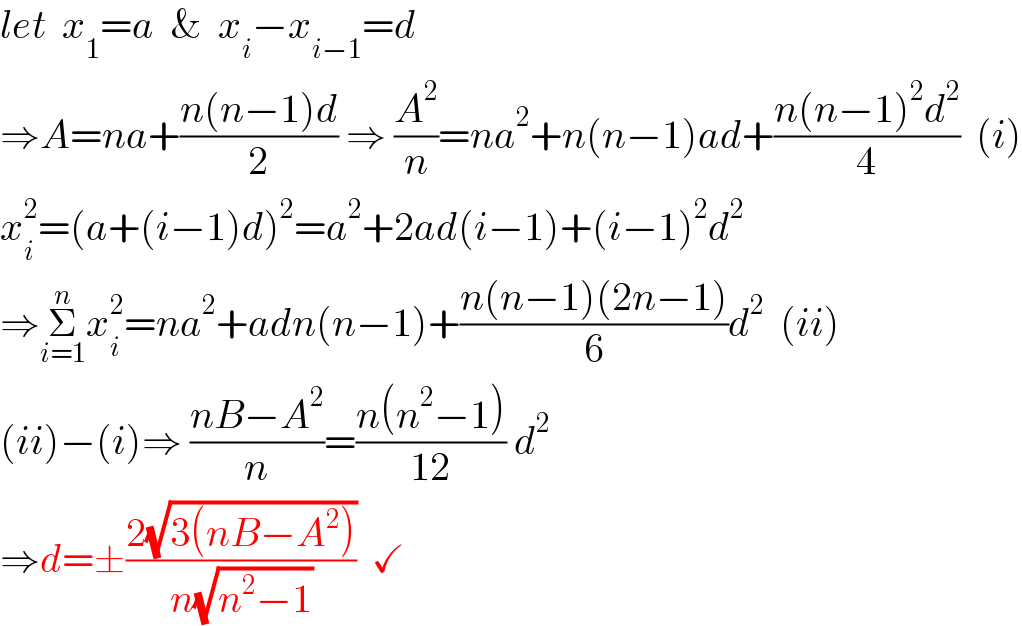
$${let}\:\:{x}_{\mathrm{1}} ={a}\:\:\&\:\:{x}_{{i}} −{x}_{{i}−\mathrm{1}} ={d} \\ $$$$\Rightarrow{A}={na}+\frac{{n}\left({n}−\mathrm{1}\right){d}}{\mathrm{2}}\:\Rightarrow\:\frac{{A}^{\mathrm{2}} }{{n}}={na}^{\mathrm{2}} +{n}\left({n}−\mathrm{1}\right){ad}+\frac{{n}\left({n}−\mathrm{1}\right)^{\mathrm{2}} {d}^{\mathrm{2}} }{\mathrm{4}}\:\:\left({i}\right) \\ $$$${x}_{{i}} ^{\mathrm{2}} =\left({a}+\left({i}−\mathrm{1}\right){d}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{2}{ad}\left({i}−\mathrm{1}\right)+\left({i}−\mathrm{1}\right)^{\mathrm{2}} {d}^{\mathrm{2}} \\ $$$$\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{\mathrm{2}} ={na}^{\mathrm{2}} +{adn}\left({n}−\mathrm{1}\right)+\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}{d}^{\mathrm{2}} \:\:\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right)\Rightarrow\:\frac{{nB}−{A}^{\mathrm{2}} }{{n}}=\frac{{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{12}}\:{d}^{\mathrm{2}} \\ $$$$\Rightarrow{d}=\pm\frac{\mathrm{2}\sqrt{\mathrm{3}\left({nB}−{A}^{\mathrm{2}} \right)}}{{n}\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}\:\:\checkmark\: \\ $$
