Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199194 by hardmath last updated on 29/Oct/23

a_1 ,a_2 ,... a_1 =1 a_(2n) =n∙a_n a_2^(100) = ?

$$\mathrm{a}_{\mathrm{1}} ,\mathrm{a}_{\mathrm{2}} ,... \\ $$$$\mathrm{a}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{2n}} =\mathrm{n}\centerdot\mathrm{a}_{\mathrm{n}} \\ $$$$\mathrm{a}_{\mathrm{2}^{\mathrm{100}} } \:=\:? \\ $$

Answered by mr W last updated on 29/Oct/23

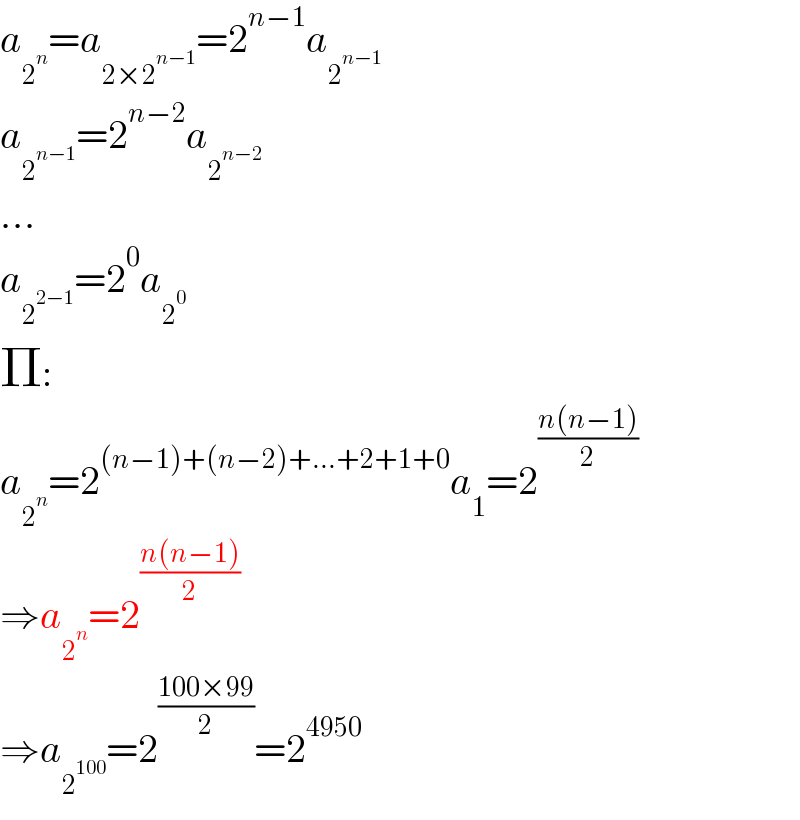
a_2^n =a_(2×2^(n−1) ) =2^(n−1) a_2^(n−1) a_2^(n−1) =2^(n−2) a_2^(n−2) ... a_2^(2−1) =2^0 a_2^0 Π: a_2^n =2^((n−1)+(n−2)+...+2+1+0) a_1 =2^((n(n−1))/2) ⇒a_2^n =2^((n(n−1))/2) ⇒a_2^(100) =2^((100×99)/2) =2^(4950)

$${a}_{\mathrm{2}^{{n}} } ={a}_{\mathrm{2}×\mathrm{2}^{{n}−\mathrm{1}} } =\mathrm{2}^{{n}−\mathrm{1}} {a}_{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{2}^{{n}−\mathrm{1}} } =\mathrm{2}^{{n}−\mathrm{2}} {a}_{\mathrm{2}^{{n}−\mathrm{2}} } \\ $$$$... \\ $$$${a}_{\mathrm{2}^{\mathrm{2}−\mathrm{1}} } =\mathrm{2}^{\mathrm{0}} {a}_{\mathrm{2}^{\mathrm{0}} } \\ $$$$\Pi: \\ $$$${a}_{\mathrm{2}^{{n}} } =\mathrm{2}^{\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{2}\right)+...+\mathrm{2}+\mathrm{1}+\mathrm{0}} {a}_{\mathrm{1}} =\mathrm{2}^{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\Rightarrow{a}_{\mathrm{2}^{{n}} } =\mathrm{2}^{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\Rightarrow{a}_{\mathrm{2}^{\mathrm{100}} } =\mathrm{2}^{\frac{\mathrm{100}×\mathrm{99}}{\mathrm{2}}} =\mathrm{2}^{\mathrm{4950}} \\ $$

Commented by hardmath last updated on 29/Oct/23

perfect dear professor thank you

$$\mathrm{perfect}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com