Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217643 by Rojarani last updated on 17/Mar/25

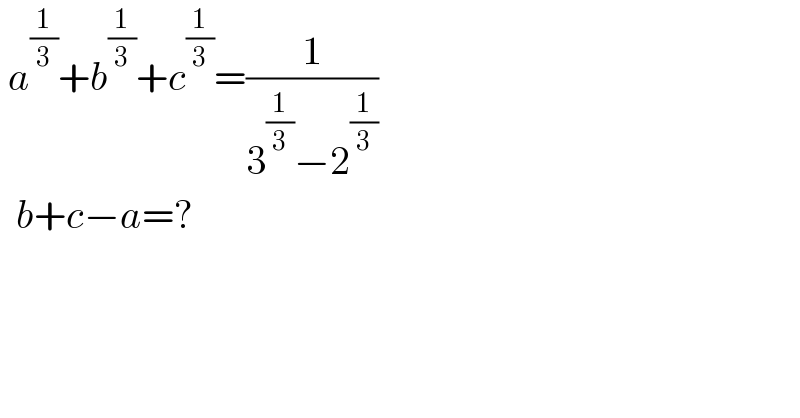
a^(1/3) +b^(1/3) +c^(1/3) =(1/(3^(1/3) −2^(1/3) )) b+c−a=?

$$\:{a}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\:\:{b}+{c}−{a}=? \\ $$

Answered by mehdee7396 last updated on 17/Mar/25

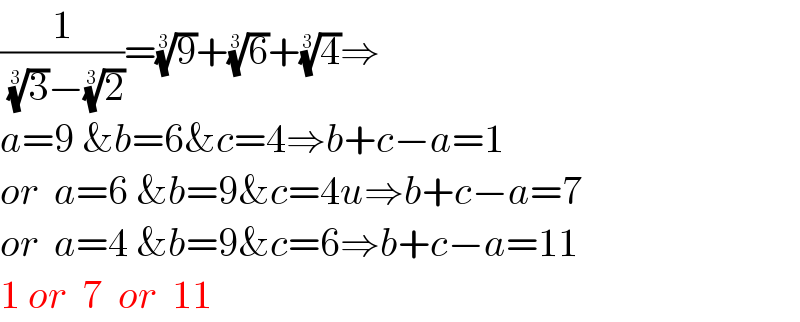
(1/( (3)^(1/3) −(2)^(1/3) ))=(9)^(1/3) +(6)^(1/3) +(4)^(1/3) ⇒ a=9 &b=6&c=4⇒b+c−a=1 or a=6 &b=9&c=4u⇒b+c−a=7 or a=4 &b=9&c=6⇒b+c−a=11 1 or 7 or 11

$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}=\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{6}}+\sqrt[{\mathrm{3}}]{\mathrm{4}}\Rightarrow \\ $$$${a}=\mathrm{9}\:\&{b}=\mathrm{6\&}{c}=\mathrm{4}\Rightarrow{b}+{c}−{a}=\mathrm{1} \\ $$$${or}\:\:{a}=\mathrm{6}\:\&{b}=\mathrm{9\&}{c}=\mathrm{4}{u}\Rightarrow{b}+{c}−{a}=\mathrm{7} \\ $$$${or}\:\:{a}=\mathrm{4}\:\&{b}=\mathrm{9\&}{c}=\mathrm{6}\Rightarrow{b}+{c}−{a}=\mathrm{11} \\ $$$$\mathrm{1}\:{or}\:\:\mathrm{7}\:\:{or}\:\:\mathrm{11} \\ $$

Commented by Rojarani last updated on 17/Mar/25

Sir thanks.

$${Sir}\:{thanks}. \\ $$

Answered by Rasheed.Sindhi last updated on 17/Mar/25

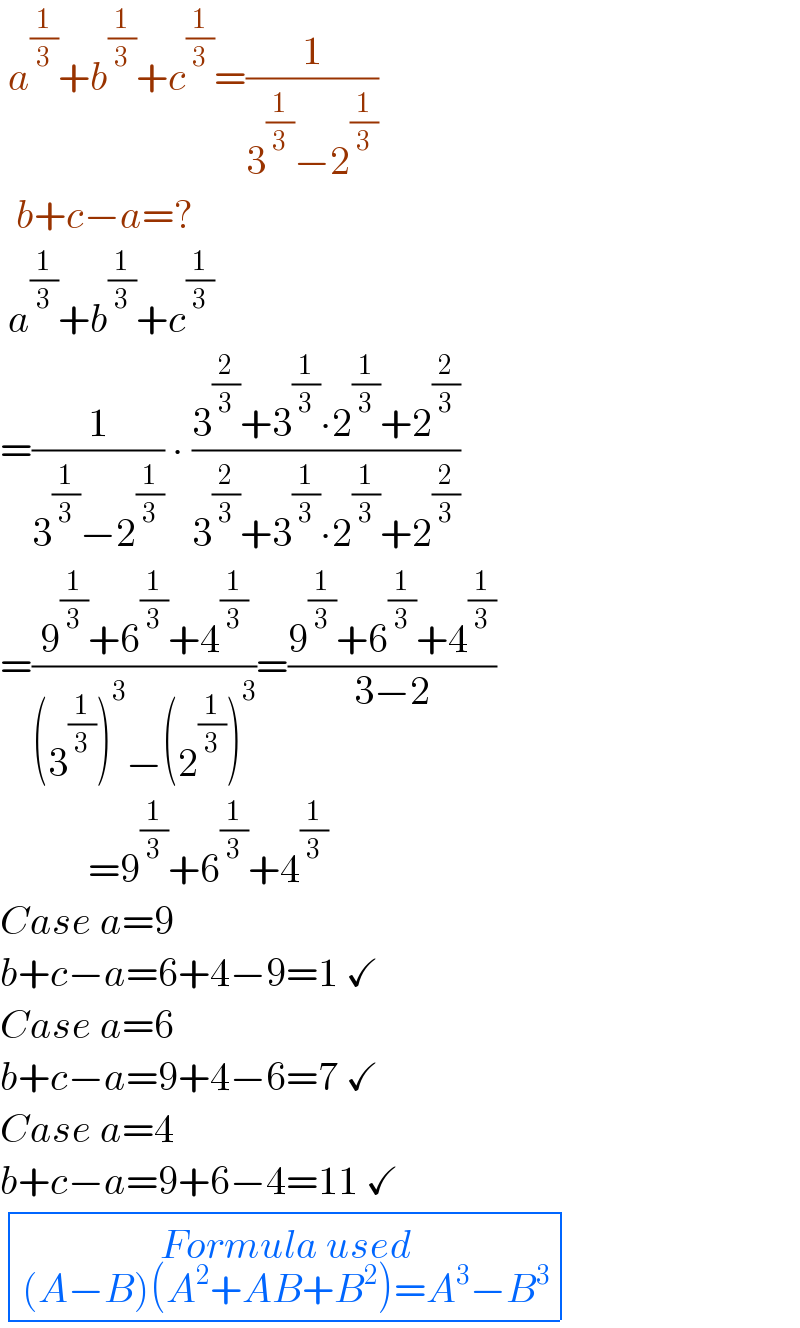
a^(1/3) +b^(1/3) +c^(1/3) =(1/(3^(1/3) −2^(1/3) )) b+c−a=? a^(1/3) +b^(1/3) +c^(1/3) =(1/(3^(1/3) −2^(1/3) )) ∙ ((3^(2/3) +3^(1/3) ∙2^(1/3) +2^(2/3) )/(3^(2/3) +3^(1/3) ∙2^(1/3) +2^(2/3) )) =((9^(1/3) +6^(1/3) +4^(1/3) )/((3^(1/3) )^3 −(2^(1/3) )^3 ))=((9^(1/3) +6^(1/3) +4^(1/3) )/(3−2)) =9^(1/3) +6^(1/3) +4^(1/3) Case a=9 b+c−a=6+4−9=1 ✓ Case a=6 b+c−a=9+4−6=7 ✓ Case a=4 b+c−a=9+6−4=11 ✓ determinant ((((A−B)(A^2 +AB+B^2 )=A^3 −B^3 ^(Formula used) )))

$$\:{a}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\:\:{b}+{c}−{a}=? \\ $$$$\:{a}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{1}}{\mathrm{3}}} +{c}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\centerdot\:\frac{\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \centerdot\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\left(\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)^{\mathrm{3}} −\left(\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)^{\mathrm{3}} }=\frac{\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{3}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${Case}\:{a}=\mathrm{9} \\ $$$${b}+{c}−{a}=\mathrm{6}+\mathrm{4}−\mathrm{9}=\mathrm{1}\:\checkmark \\ $$$${Case}\:{a}=\mathrm{6} \\ $$$${b}+{c}−{a}=\mathrm{9}+\mathrm{4}−\mathrm{6}=\mathrm{7}\:\checkmark \\ $$$${Case}\:{a}=\mathrm{4} \\ $$$${b}+{c}−{a}=\mathrm{9}+\mathrm{6}−\mathrm{4}=\mathrm{11}\:\checkmark \\ $$$$\begin{array}{|c|}{\overset{{Formula}\:{used}} {\left({A}−{B}\right)\left({A}^{\mathrm{2}} +{AB}+{B}^{\mathrm{2}} \right)={A}^{\mathrm{3}} −{B}^{\mathrm{3}} }}\\\hline\end{array} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com