
Question Number 219408 by CrispyXYZ last updated on 24/Apr/25
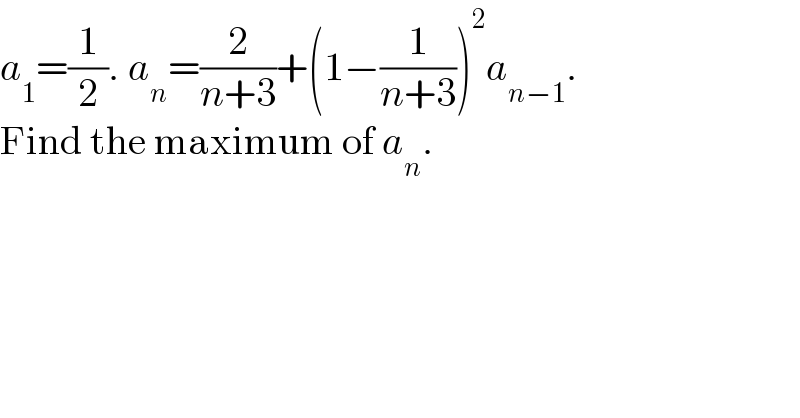
$${a}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}.\:{a}_{{n}} =\frac{\mathrm{2}}{{n}+\mathrm{3}}+\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)^{\mathrm{2}} {a}_{{n}−\mathrm{1}} . \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{of}\:{a}_{{n}} . \\ $$
Answered by SdC355 last updated on 24/Apr/25
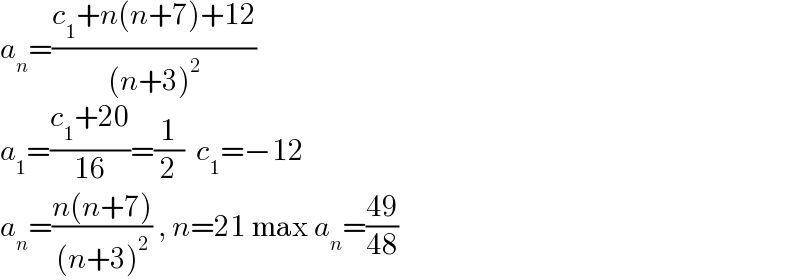
$${a}_{{n}} =\frac{{c}_{\mathrm{1}} +{n}\left({n}+\mathrm{7}\right)+\mathrm{12}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${a}_{\mathrm{1}} =\frac{{c}_{\mathrm{1}} +\mathrm{20}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{2}}\:\:{c}_{\mathrm{1}} =−\mathrm{12} \\ $$$${a}_{{n}} =\frac{{n}\left({n}+\mathrm{7}\right)}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }\:,\:{n}=\mathrm{21}\:\mathrm{max}\:{a}_{{n}} =\frac{\mathrm{49}}{\mathrm{48}} \\ $$
Commented by universe last updated on 24/Apr/25
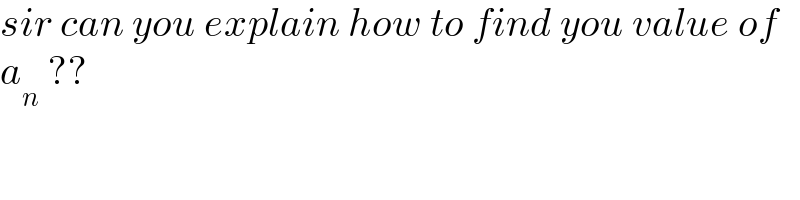
$${sir}\:{can}\:{you}\:{explain}\:{how}\:{to}\:{find}\:{you}\:{value}\:{of} \\ $$$${a}_{{n}} \:?? \\ $$
Answered by universe last updated on 24/Apr/25

