
Question Number 6609 by Temp last updated on 05/Jul/16
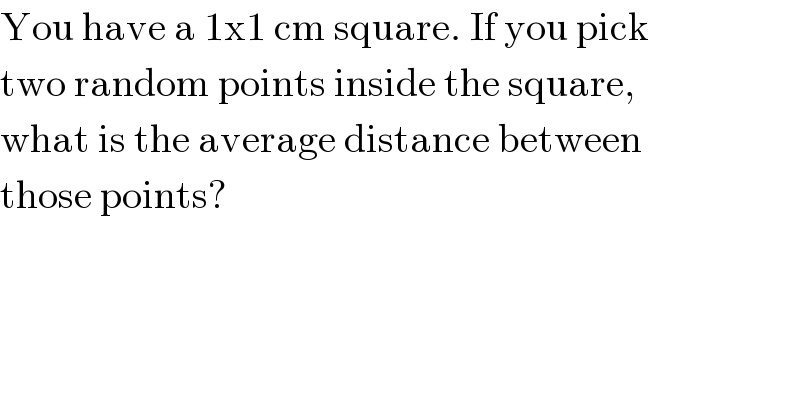
$$\mathrm{You}\:\mathrm{have}\:\mathrm{a}\:\mathrm{1x1}\:\mathrm{cm}\:\mathrm{square}.\:\mathrm{If}\:\mathrm{you}\:\mathrm{pick} \\ $$$$\mathrm{two}\:\mathrm{random}\:\mathrm{points}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{square}, \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{average}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{those}\:\mathrm{points}? \\ $$
Commented by prakash jain last updated on 05/Jul/16

$$\mathrm{Let}\:{X}\:\mathrm{and}\:{Y}\:\mathrm{be}\:\mathrm{two}\:\mathrm{random}\:\mathrm{variable}. \\ $$$${f}_{{X}} \left({x}\right)\:\mathrm{and}\:{f}_{{Y}} \left({y}\right)\:\mathrm{are}\:\mathrm{probability}\:\mathrm{density}\:\mathrm{function} \\ $$$$\mathrm{of}\:\mathrm{X}\:\mathrm{and}\:\mathrm{Y}.\: \\ $$$$ \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{above}\:\mathrm{case}\:\mathrm{we}\:\mathrm{can}\:\mathrm{assume}\:\mathrm{uniform}. \\ $$$$\mathrm{We}\:\mathrm{define}\:\mathrm{a}\:\mathrm{new}\:\mathrm{random}\:\mathrm{variable} \\ $$$${Z}=\sqrt{{X}^{\mathrm{2}} +{Y}^{\mathrm{2}} } \\ $$$$\mathrm{Then}\:\mathrm{mean}\:\mathrm{value}\:\mathrm{of}\:{Z}\:\mathrm{will}\:\mathrm{be}\:\mathrm{given}\:\mathrm{by}: \\ $$$${E}\left({Z}\right)=\int{Zf}_{{Z}} \left({z}\right){dz} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:{f}_{{Z}} \left({z}\right)\:\mathrm{from}\:{f}_{{X}} \:\mathrm{and}\:{f}_{{Y}} . \\ $$$$\mathrm{will}\:\mathrm{continue}\:\mathrm{to}\:\mathrm{find}\:{f}_{{Z}} \left({z}\right) \\ $$
Commented by prakash jain last updated on 05/Jul/16
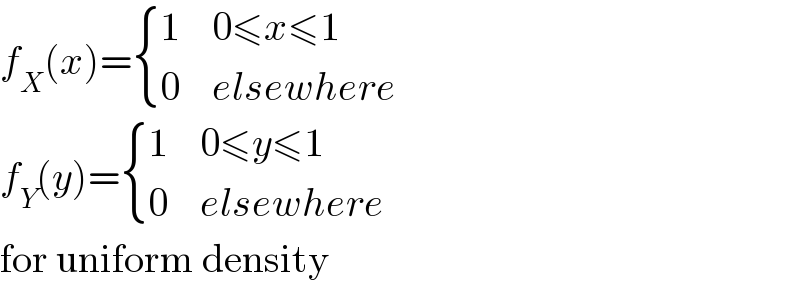
$${f}_{{X}} \left({x}\right)=\begin{cases}{\mathrm{1}}&{\mathrm{0}\leqslant{x}\leqslant\mathrm{1}}\\{\mathrm{0}}&{{elsewhere}}\end{cases} \\ $$$${f}_{{Y}} \left({y}\right)=\begin{cases}{\mathrm{1}}&{\mathrm{0}\leqslant{y}\leqslant\mathrm{1}}\\{\mathrm{0}}&{{elsewhere}}\end{cases} \\ $$$$\mathrm{for}\:\mathrm{uniform}\:\mathrm{density} \\ $$
Commented by prakash jain last updated on 05/Jul/16

$$\mathrm{Since}\:{X}\:\mathrm{and}\:{Y}\:\mathrm{are}\:\mathrm{independent}\:\mathrm{variable} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{write}\:\mathrm{joint}\:\mathrm{probablity}\:\mathrm{distribution} \\ $$$$\mathrm{as} \\ $$$${f}_{{XY}} \left({x},{y}\right)={f}_{{X}} \left({x}\right)\centerdot{f}_{{Y}} \left({y}\right) \\ $$$$\mathrm{Expected}\:\mathrm{value}\:\mathrm{of}\:\mathrm{distance} \\ $$$${z}={g}\left({x},{y}\right)=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${E}\left({g}\left({x},{y}\right)\right)=\int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{f}_{{X}} \left({x}\right){f}_{{Y}} \left({y}\right){dxdy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dxdy}=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{sinh}^{−\mathrm{1}} \mathrm{1}\right) \\ $$$$\mathrm{Please}\:\mathrm{check}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{100\%}\:\mathrm{sure}. \\ $$
Commented by Temp last updated on 05/Jul/16
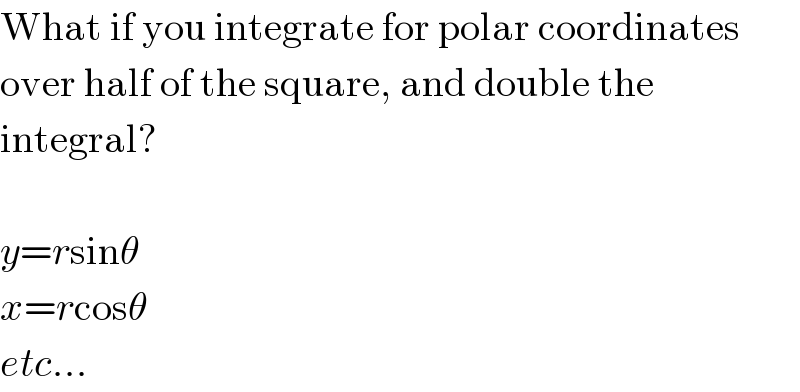
$$\mathrm{What}\:\mathrm{if}\:\mathrm{you}\:\mathrm{integrate}\:\mathrm{for}\:\mathrm{polar}\:\mathrm{coordinates} \\ $$$$\mathrm{over}\:\mathrm{half}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square},\:\mathrm{and}\:\mathrm{double}\:\mathrm{the} \\ $$$$\mathrm{integral}? \\ $$$$ \\ $$$${y}={r}\mathrm{sin}\theta \\ $$$${x}={r}\mathrm{cos}\theta \\ $$$${etc}... \\ $$
Commented by prakash jain last updated on 07/Jul/16
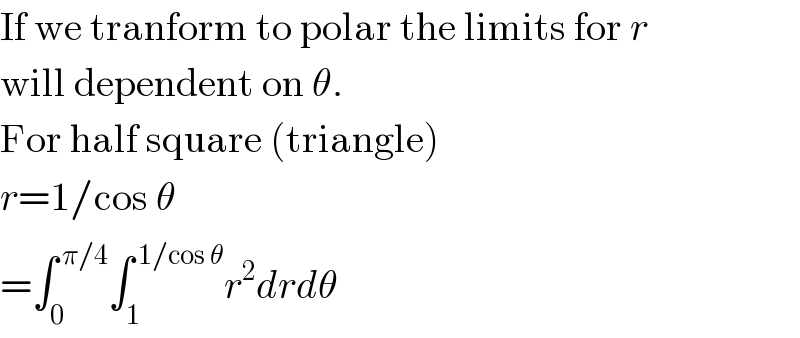
$$\mathrm{If}\:\mathrm{we}\:\mathrm{tranform}\:\mathrm{to}\:\mathrm{polar}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{for}\:{r} \\ $$$$\mathrm{will}\:\mathrm{dependent}\:\mathrm{on}\:\theta. \\ $$$$\mathrm{For}\:\mathrm{half}\:\mathrm{square}\:\left(\mathrm{triangle}\right) \\ $$$${r}=\mathrm{1}/\mathrm{cos}\:\theta \\ $$$$=\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \int_{\mathrm{1}} ^{\:\mathrm{1}/\mathrm{cos}\:\theta} {r}^{\mathrm{2}} {drd}\theta \\ $$
