
Question Number 208158 by necx122 last updated on 06/Jun/24
$${X},\:{Y}\:{and}\:{Z}\:{are}\:{points}\:{on}\:{the}\:{sides}\:{AB}, \\ $$$${BC}\:{and}\:{AC}\:{of}\:{the}\:{triangle}\:{ABC},\:{such} \\ $$$${that}\:{AX}:{XB}\:=\mathrm{4}:\mathrm{3},\:{BY}:{YC}=\mathrm{2}:\mathrm{3},\: \\ $$$${CZ}:{ZA}=\mathrm{2}:\mathrm{1}.\:{Find}\:{the}\:{ratio}\:{of}\:{the}\:{area} \\ $$$${of}\:{the}\:{triangle}\:{XYZ}\:{to}\:{that}\:{of}\:{triangle} \\ $$$${ABC}. \\ $$
Answered by mr W last updated on 06/Jun/24
Commented by mr W last updated on 06/Jun/24
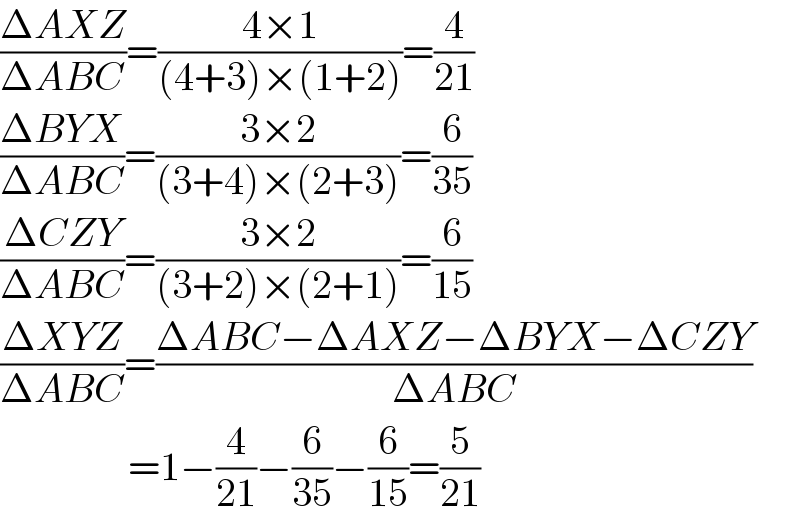
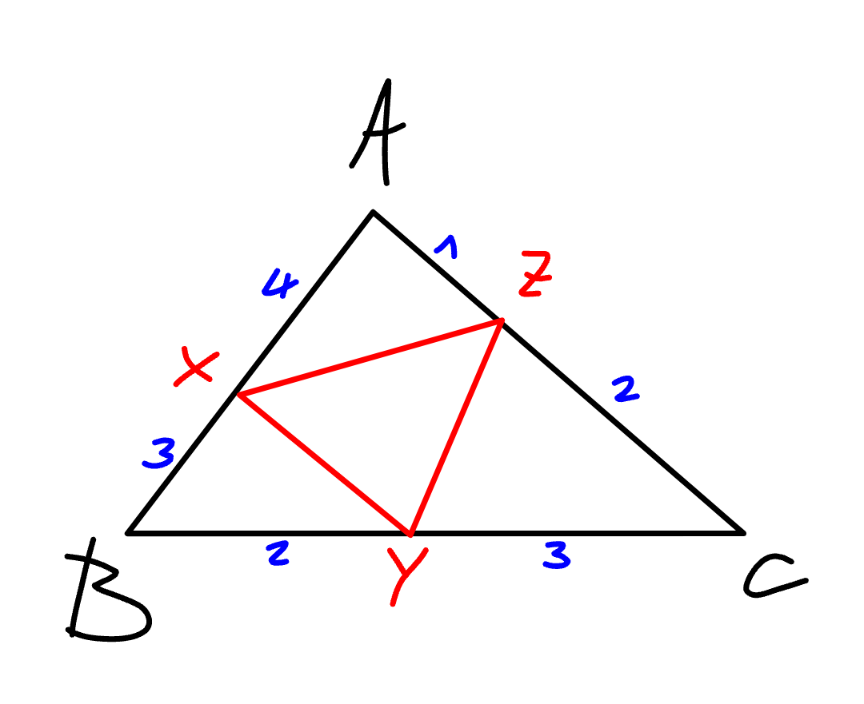
$$\frac{\Delta{AXZ}}{\Delta{ABC}}=\frac{\mathrm{4}×\mathrm{1}}{\left(\mathrm{4}+\mathrm{3}\right)×\left(\mathrm{1}+\mathrm{2}\right)}=\frac{\mathrm{4}}{\mathrm{21}} \\ $$$$\frac{\Delta{BYX}}{\Delta{ABC}}=\frac{\mathrm{3}×\mathrm{2}}{\left(\mathrm{3}+\mathrm{4}\right)×\left(\mathrm{2}+\mathrm{3}\right)}=\frac{\mathrm{6}}{\mathrm{35}} \\ $$$$\frac{\Delta{CZY}}{\Delta{ABC}}=\frac{\mathrm{3}×\mathrm{2}}{\left(\mathrm{3}+\mathrm{2}\right)×\left(\mathrm{2}+\mathrm{1}\right)}=\frac{\mathrm{6}}{\mathrm{15}} \\ $$$$\frac{\Delta{XYZ}}{\Delta{ABC}}=\frac{\Delta{ABC}−\Delta{AXZ}−\Delta{BYX}−\Delta{CZY}}{\Delta{ABC}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{21}}−\frac{\mathrm{6}}{\mathrm{35}}−\frac{\mathrm{6}}{\mathrm{15}}=\frac{\mathrm{5}}{\mathrm{21}} \\ $$
Commented by Ari last updated on 07/Jun/24

Commented by mr W last updated on 07/Jun/24
Commented by mr W last updated on 07/Jun/24
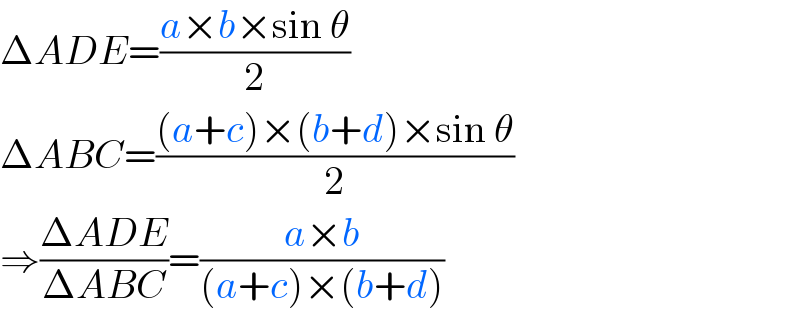
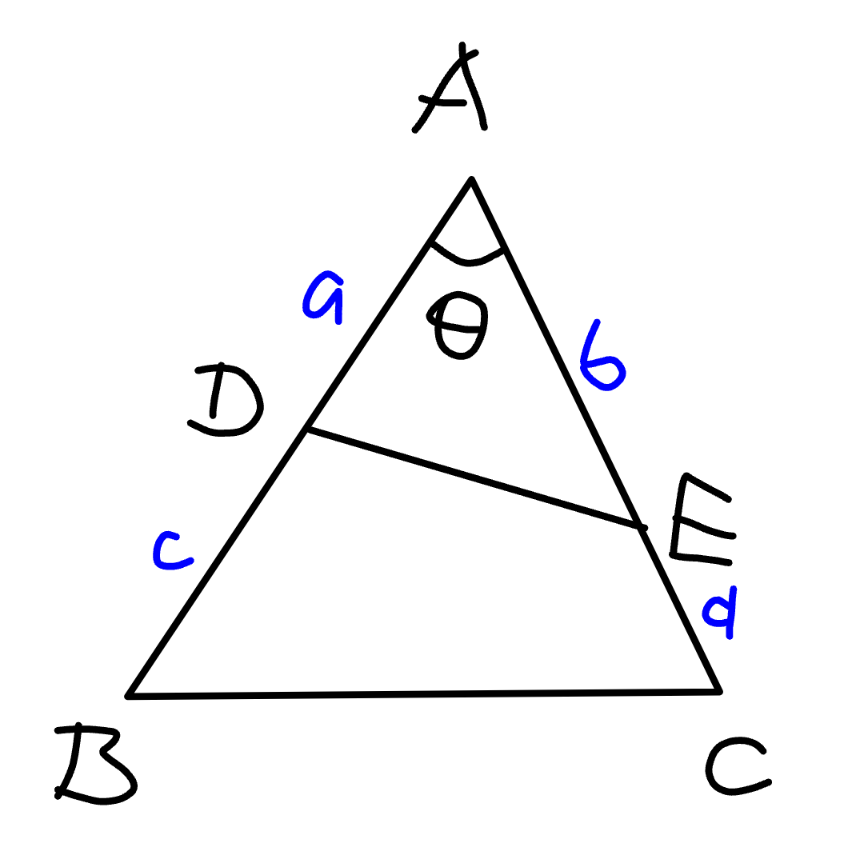
$$\Delta{ADE}=\frac{{a}×{b}×\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Delta{ABC}=\frac{\left({a}+{c}\right)×\left({b}+{d}\right)×\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\Delta{ADE}}{\Delta{ABC}}=\frac{{a}×{b}}{\left({a}+{c}\right)×\left({b}+{d}\right)} \\ $$
Commented by necx122 last updated on 07/Jun/24
$${This}\:{is}\:{really}\:{cool}. \\ $$
Commented by Ari last updated on 08/Jun/24

$${thank}\:{you}\:{Sir}! \\ $$
Commented by Tawa11 last updated on 21/Jun/24

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
