
Question Number 59305 by pete last updated on 07/May/19

$$\mathrm{Witthout}\:\mathrm{using}\:\mathrm{mathematical}\:\mathrm{tables}\:\mathrm{or} \\ $$$$\mathrm{calculator},\:\mathrm{find},\mathrm{in}\:\mathrm{surdform}\left(\mathrm{radicals}\right) \\ $$$$,\:\mathrm{the}\:\mathrm{value}\:\mathrm{tan22}.\mathrm{5}° \\ $$
Answered by ajfour last updated on 07/May/19
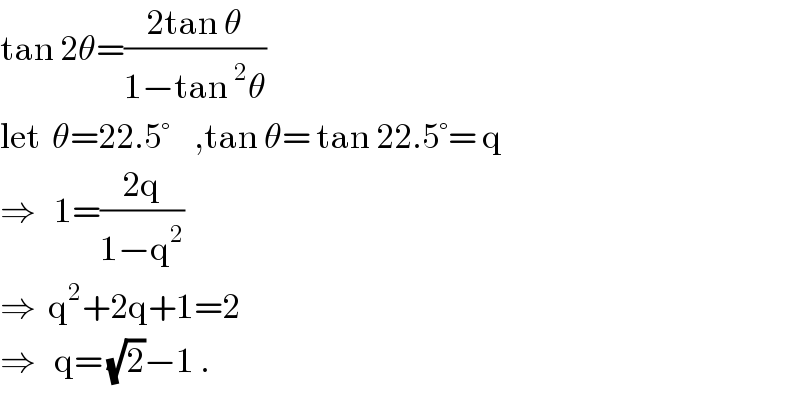
$$\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{2tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$$\mathrm{let}\:\:\theta=\mathrm{22}.\mathrm{5}°\:\:\:\:,\mathrm{tan}\:\theta=\:\mathrm{tan}\:\mathrm{22}.\mathrm{5}°=\:\mathrm{q} \\ $$$$\Rightarrow\:\:\:\mathrm{1}=\frac{\mathrm{2q}}{\mathrm{1}−\mathrm{q}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{q}^{\mathrm{2}} +\mathrm{2q}+\mathrm{1}=\mathrm{2} \\ $$$$\Rightarrow\:\:\:\mathrm{q}=\:\sqrt{\mathrm{2}}−\mathrm{1}\:. \\ $$
Commented by pete last updated on 08/May/19

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by malwaan last updated on 08/May/19

$${tan}\frac{\theta}{\mathrm{2}}=\pm\sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{1}+{sin}\theta}} \\ $$$${tan}\mathrm{22}.\mathrm{5}={tan}\frac{\mathrm{45}}{\mathrm{2}}=+\sqrt{\frac{\mathrm{1}−{cos}\:\mathrm{45}^{°} }{\mathrm{1}+{cos}\:\mathrm{45}^{°} }} \\ $$$$\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}}=\sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$$=\sqrt{\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}−\mathrm{2}}}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{2}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$
Commented by pete last updated on 11/May/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{boss} \\ $$
