Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 5495 by FilupSmith last updated on 16/May/16

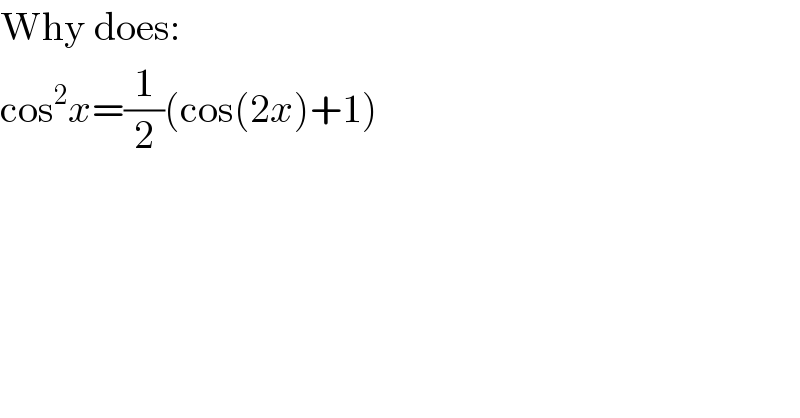
Why does: cos^2 x=(1/2)(cos(2x)+1)

$$\mathrm{Why}\:\mathrm{does}: \\ $$$$\mathrm{cos}^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right) \\ $$

Commented by Yozzii last updated on 16/May/16

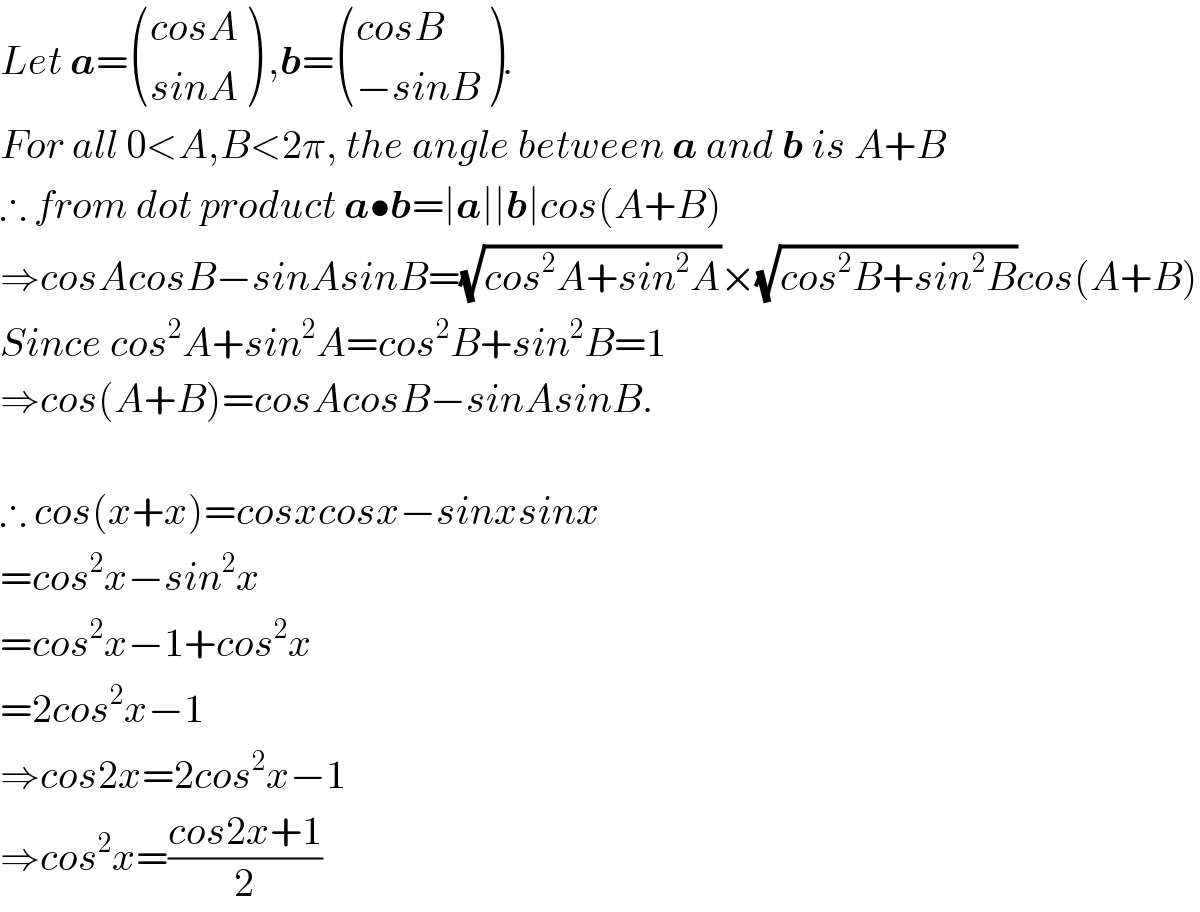
Let a= (((cosA)),((sinA)) ) ,b= (((cosB)),((−sinB)) ). For all 0<A,B<2π, the angle between a and b is A+B ∴ from dot product a•b=∣a∣∣b∣cos(A+B) ⇒cosAcosB−sinAsinB=(√(cos^2 A+sin^2 A))×(√(cos^2 B+sin^2 B))cos(A+B) Since cos^2 A+sin^2 A=cos^2 B+sin^2 B=1 ⇒cos(A+B)=cosAcosB−sinAsinB. ∴ cos(x+x)=cosxcosx−sinxsinx =cos^2 x−sin^2 x =cos^2 x−1+cos^2 x =2cos^2 x−1 ⇒cos2x=2cos^2 x−1 ⇒cos^2 x=((cos2x+1)/2)

$${Let}\:\boldsymbol{{a}}=\begin{pmatrix}{{cosA}}\\{{sinA}}\end{pmatrix}\:,\boldsymbol{{b}}=\begin{pmatrix}{{cosB}}\\{−{sinB}}\end{pmatrix}. \\ $$$${For}\:{all}\:\mathrm{0}<{A},{B}<\mathrm{2}\pi,\:{the}\:{angle}\:{between}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}\:{is}\:{A}+{B} \\ $$$$\therefore\:{from}\:{dot}\:{product}\:\boldsymbol{{a}}\bullet\boldsymbol{{b}}=\mid\boldsymbol{{a}}\mid\mid\boldsymbol{{b}}\mid{cos}\left({A}+{B}\right) \\ $$$$\Rightarrow{cosAcosB}−{sinAsinB}=\sqrt{{cos}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} {A}}×\sqrt{{cos}^{\mathrm{2}} {B}+{sin}^{\mathrm{2}} {B}}{cos}\left({A}+{B}\right) \\ $$$${Since}\:{cos}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} {A}={cos}^{\mathrm{2}} {B}+{sin}^{\mathrm{2}} {B}=\mathrm{1} \\ $$$$\Rightarrow{cos}\left({A}+{B}\right)={cosAcosB}−{sinAsinB}. \\ $$$$ \\ $$$$\therefore\:{cos}\left({x}+{x}\right)={cosxcosx}−{sinxsinx} \\ $$$$={cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x} \\ $$$$={cos}^{\mathrm{2}} {x}−\mathrm{1}+{cos}^{\mathrm{2}} {x} \\ $$$$=\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1} \\ $$$$\Rightarrow{cos}\mathrm{2}{x}=\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} {x}=\frac{{cos}\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}} \\ $$

Answered by Rasheed Soomro last updated on 16/May/16

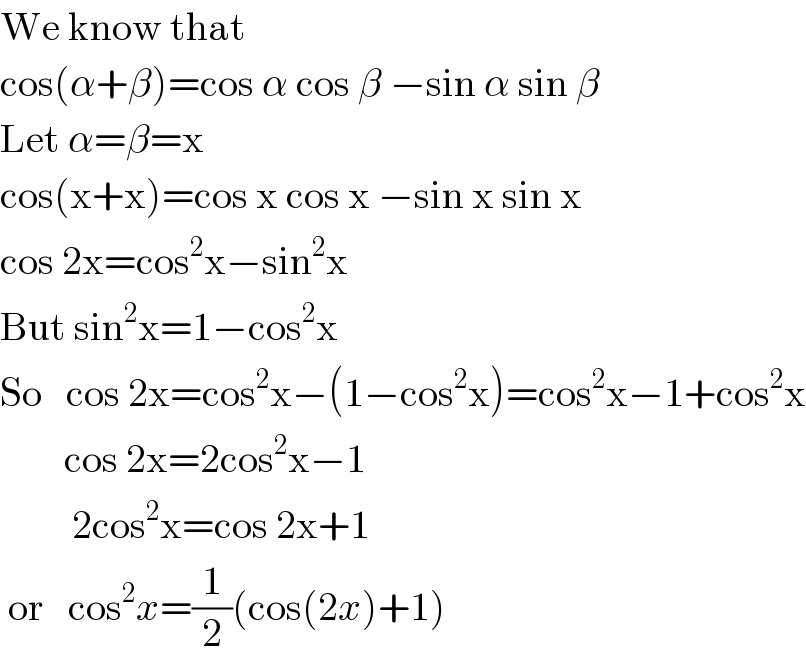
We know that cos(α+β)=cos α cos β −sin α sin β Let α=β=x cos(x+x)=cos x cos x −sin x sin x cos 2x=cos^2 x−sin^2 x But sin^2 x=1−cos^2 x So cos 2x=cos^2 x−(1−cos^2 x)=cos^2 x−1+cos^2 x cos 2x=2cos^2 x−1 2cos^2 x=cos 2x+1 or cos^2 x=(1/2)(cos(2x)+1)

$$\mathrm{We}\:\mathrm{know}\:\mathrm{that} \\ $$$$\mathrm{cos}\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta \\ $$$$\mathrm{Let}\:\alpha=\beta=\mathrm{x} \\ $$$$\mathrm{cos}\left(\mathrm{x}+\mathrm{x}\right)=\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:−\mathrm{sin}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{cos}\:\mathrm{2x}=\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{But}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}=\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{So}\:\:\:\mathrm{cos}\:\mathrm{2x}=\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)=\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{2x}=\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2cos}^{\mathrm{2}} \mathrm{x}=\mathrm{cos}\:\mathrm{2x}+\mathrm{1} \\ $$$$\:\mathrm{or}\:\:\:\mathrm{cos}^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com