
Question Number 183535 by HeferH last updated on 26/Dec/22
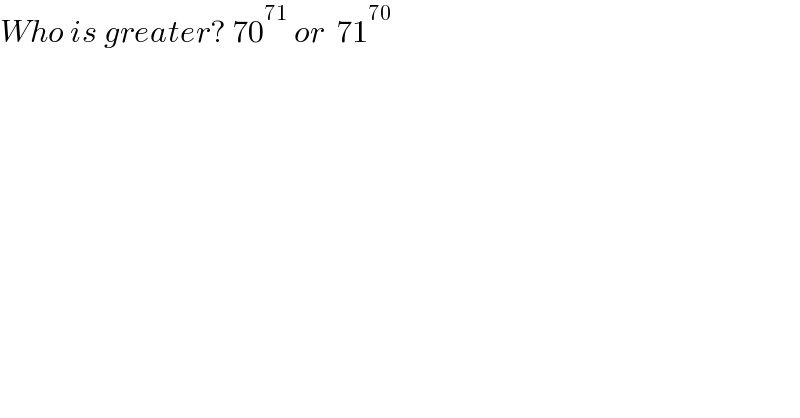
$${Who}\:{is}\:{greater}?\:\mathrm{70}^{\mathrm{71}} \:{or}\:\:\mathrm{71}^{\mathrm{70}} \\ $$
Answered by Frix last updated on 26/Dec/22
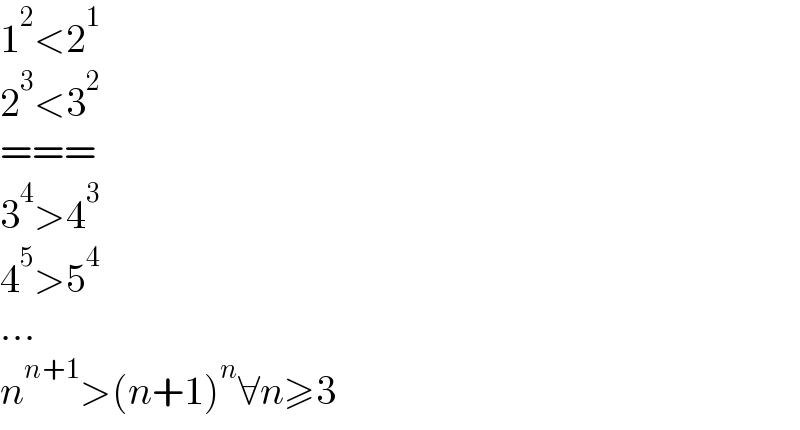
$$\mathrm{1}^{\mathrm{2}} <\mathrm{2}^{\mathrm{1}} \\ $$$$\mathrm{2}^{\mathrm{3}} <\mathrm{3}^{\mathrm{2}} \\ $$$$=== \\ $$$$\mathrm{3}^{\mathrm{4}} >\mathrm{4}^{\mathrm{3}} \\ $$$$\mathrm{4}^{\mathrm{5}} >\mathrm{5}^{\mathrm{4}} \\ $$$$... \\ $$$${n}^{{n}+\mathrm{1}} >\left({n}+\mathrm{1}\right)^{{n}} \forall{n}\geqslant\mathrm{3} \\ $$
Commented by HeferH last updated on 26/Dec/22

$$\left.{thanks}\::\right) \\ $$
Answered by mr W last updated on 26/Dec/22
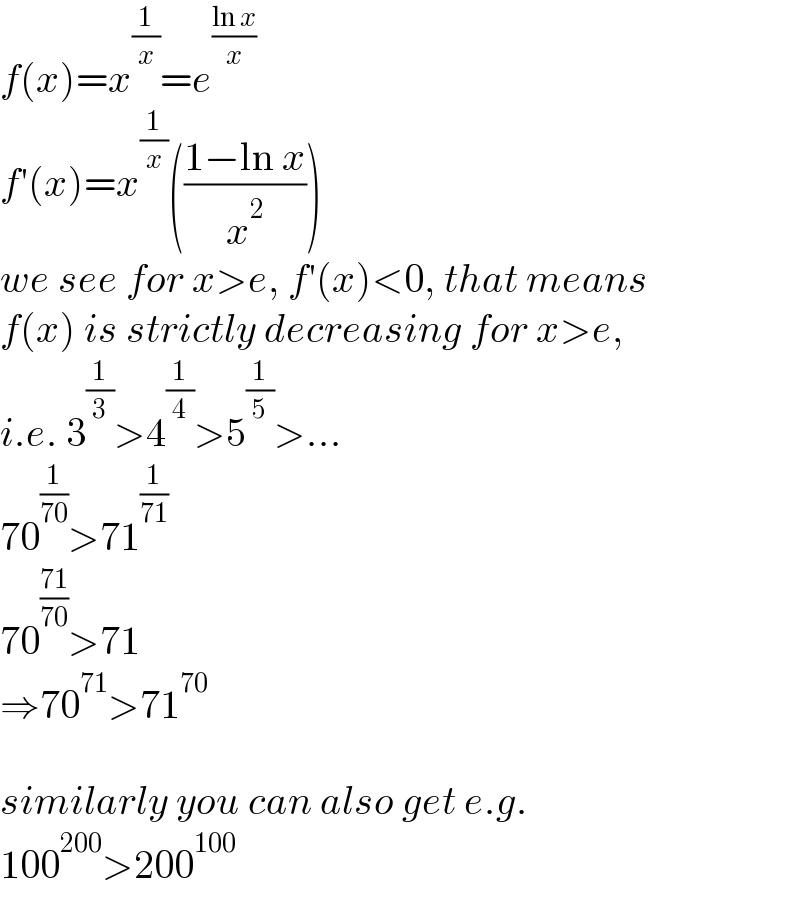
$${f}\left({x}\right)={x}^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{ln}\:{x}}{{x}}} \\ $$$${f}'\left({x}\right)={x}^{\frac{\mathrm{1}}{{x}}} \left(\frac{\mathrm{1}−\mathrm{ln}\:{x}}{{x}^{\mathrm{2}} }\right) \\ $$$${we}\:{see}\:{for}\:{x}>{e},\:{f}'\left({x}\right)<\mathrm{0},\:{that}\:{means} \\ $$$${f}\left({x}\right)\:{is}\:{strictly}\:{decreasing}\:{for}\:{x}>{e}, \\ $$$${i}.{e}.\:\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} >\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{4}}} >\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{5}}} >... \\ $$$$\mathrm{70}^{\frac{\mathrm{1}}{\mathrm{70}}} >\mathrm{71}^{\frac{\mathrm{1}}{\mathrm{71}}} \\ $$$$\mathrm{70}^{\frac{\mathrm{71}}{\mathrm{70}}} >\mathrm{71} \\ $$$$\Rightarrow\mathrm{70}^{\mathrm{71}} >\mathrm{71}^{\mathrm{70}} \\ $$$$ \\ $$$${similarly}\:{you}\:{can}\:{also}\:{get}\:{e}.{g}. \\ $$$$\mathrm{100}^{\mathrm{200}} >\mathrm{200}^{\mathrm{100}} \\ $$
Commented by HeferH last updated on 26/Dec/22

$${thanks}\:! \\ $$
