
Question Number 115856 by bemath last updated on 29/Sep/20

$${Which}\:{is}\:{greater} \\ $$$${P}\:=\:\left(\mathrm{1983}\right)\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{1984}\right)\:,\:{or} \\ $$$${Q}\:=\:\left(\mathrm{1984}\right)\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{1983}\right) \\ $$
Answered by bobhans last updated on 29/Sep/20
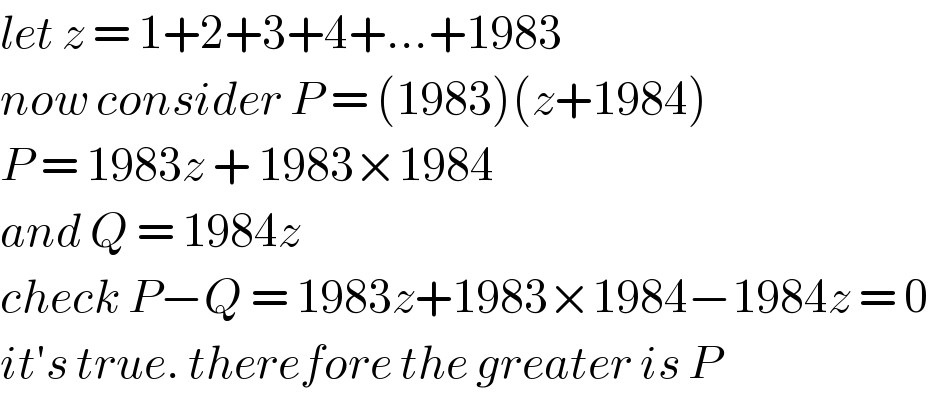
$${let}\:{z}\:=\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+\mathrm{1983} \\ $$$${now}\:{consider}\:{P}\:=\:\left(\mathrm{1983}\right)\left({z}+\mathrm{1984}\right) \\ $$$${P}\:=\:\mathrm{1983}{z}\:+\:\mathrm{1983}×\mathrm{1984} \\ $$$${and}\:{Q}\:=\:\mathrm{1984}{z}\: \\ $$$${check}\:{P}−{Q}\:=\:\mathrm{1983}{z}+\mathrm{1983}×\mathrm{1984}−\mathrm{1984}{z}\:=\:\mathrm{0} \\ $$$${it}'{s}\:{true}.\:{therefore}\:{the}\:{greater}\:{is}\:{P} \\ $$
Answered by floor(10²Eta[1]) last updated on 29/Sep/20
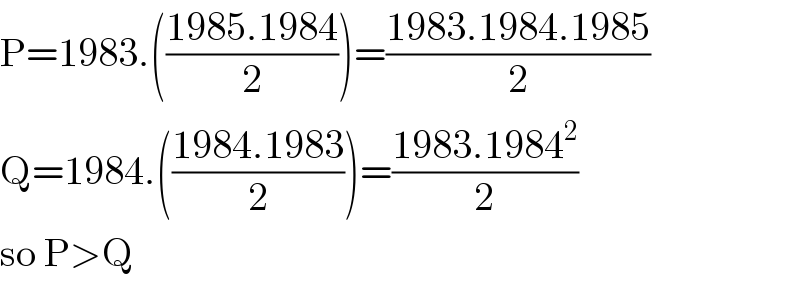
$$\mathrm{P}=\mathrm{1983}.\left(\frac{\mathrm{1985}.\mathrm{1984}}{\mathrm{2}}\right)=\frac{\mathrm{1983}.\mathrm{1984}.\mathrm{1985}}{\mathrm{2}} \\ $$$$\mathrm{Q}=\mathrm{1984}.\left(\frac{\mathrm{1984}.\mathrm{1983}}{\mathrm{2}}\right)=\frac{\mathrm{1983}.\mathrm{1984}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{P}>\mathrm{Q} \\ $$
