Question and Answers Forum

All Questions      Topic List

Logic Questions

Previous in All Question      Next in All Question      

Previous in Logic      

Question Number 217772 by yamane last updated on 20/Mar/25

Where is the error (−1)=(−1)^1 =(−1)^(2/2) =[(−1)^2 ]^(1/2) =[1]^(1/2) =(√1) =1

$${Where}\:{is}\:{the}\:{error} \\ $$$$\left(−\mathrm{1}\right)=\left(−\mathrm{1}\right)^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left[\left(−\mathrm{1}\right)^{\mathrm{2}} \right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\mathrm{1}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1} \\ $$

Commented by Ghisom last updated on 21/Mar/25

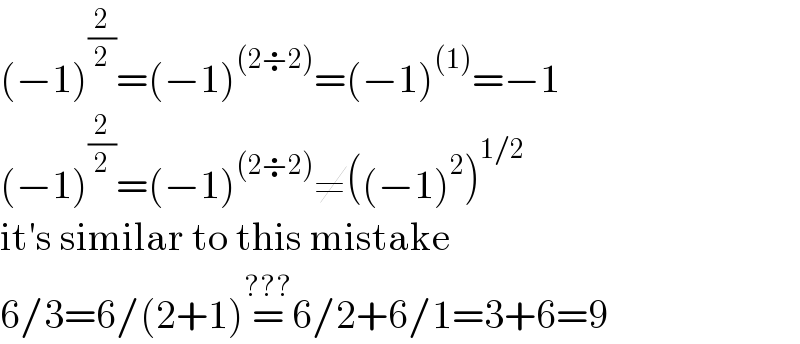
(−1)^(2/2) =(−1)^((2÷2)) =(−1)^((1)) =−1 (−1)^(2/2) =(−1)^((2÷2)) ≠((−1)^2 )^(1/2) it′s similar to this mistake 6/3=6/(2+1)=^(???) 6/2+6/1=3+6=9

$$\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} =\left(−\mathrm{1}\right)^{\left(\mathrm{2}\boldsymbol{\div}\mathrm{2}\right)} =\left(−\mathrm{1}\right)^{\left(\mathrm{1}\right)} =−\mathrm{1} \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} =\left(−\mathrm{1}\right)^{\left(\mathrm{2}\boldsymbol{\div}\mathrm{2}\right)} \neq\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{similar}\:\mathrm{to}\:\mathrm{this}\:\mathrm{mistake} \\ $$$$\mathrm{6}/\mathrm{3}=\mathrm{6}/\left(\mathrm{2}+\mathrm{1}\right)\overset{???} {=}\mathrm{6}/\mathrm{2}+\mathrm{6}/\mathrm{1}=\mathrm{3}+\mathrm{6}=\mathrm{9} \\ $$

Answered by Marzuk last updated on 20/Mar/25

(√1) = ±1 not only 1 r_1 = 1 and r_2 = −1 you could also say [(−1)^(1/2) ]^2 = i^2 = −1 so the main error is in the understanding of application the property (a^m )^n = a^(mn)

$$\sqrt{\mathrm{1}}\:\:=\:\:\pm\mathrm{1}\:{not}\:{only}\:\mathrm{1} \\ $$$${r}_{\mathrm{1}} \:=\:\mathrm{1}\:{and}\:{r}_{\mathrm{2}} \:=\:−\mathrm{1} \\ $$$${you}\:{could}\:{also}\:{say}\: \\ $$$$\left[\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right]^{\mathrm{2}} \\ $$$$=\:{i}^{\mathrm{2}} \\ $$$$=\:−\mathrm{1} \\ $$$${so}\:{the}\:{main}\:{error}\:{is}\:{in}\:{the}\:{understanding} \\ $$$${of}\:\:{application}\:{the}\:{property}\:\left({a}^{{m}} \right)^{{n}} =\:{a}^{{mn}} \\ $$

Commented by Ghisom last updated on 21/Mar/25

(√1)=1 (√1)=−1 is wrong this has been explained over and over again. we have exactly one rule of exponentials: z∈C ⇒ z=re^(iθ) with r≥0 and −π<θ≤π x∈Q (also works for x∈R, x∈C) z^x =(re^(iθ) )^x =r^x e^(ixθ) there′s no 2^(nd) result. never. if z=1∧x=(1/2): z=1e^(0i) z^x =(1e^(0i) )^(1/2) =1^(1/2) e^(0i/2) =1e^0 =1 how would you get −1?^((∗)) the mistake comes ftom solving equations where we have a different rule. x^2 =1 ⇒ x=±1 because here we′re looking for all values of x which give 1 if we square x (+1)^2 =1 (−1)^2 =1 (∗) the only exception is being made for geometric problems to stay in R, ignoring numbers ∈C (because they had not been invented yet in the age of geometry): ((−8))^(1/3) =(−8)^(1/3) =−2 we artificially take the root ∈R but for x∈C we have (−8)^(1/3) =(8e^(iπ) )^(1/3) =8^(1/3) e^(iπ/3) =2e^(iπ/3) ∉R

$$\sqrt{\mathrm{1}}=\mathrm{1} \\ $$$$\sqrt{\mathrm{1}}=−\mathrm{1}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{been}\:\mathrm{explained}\:\mathrm{over}\:\mathrm{and}\:\mathrm{over}\:\mathrm{again}. \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{rule}\:\mathrm{of}\:\mathrm{exponentials}: \\ $$$${z}\in\mathbb{C}\:\Rightarrow\:{z}={r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:{r}\geqslant\mathrm{0}\:\mathrm{and}\:−\pi<\theta\leqslant\pi \\ $$$${x}\in\mathbb{Q}\:\left(\mathrm{also}\:\mathrm{works}\:\mathrm{for}\:{x}\in\mathbb{R},\:{x}\in\mathbb{C}\right) \\ $$$${z}^{{x}} =\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)^{{x}} ={r}^{{x}} \mathrm{e}^{\mathrm{i}{x}\theta} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{result}.\:\mathrm{never}. \\ $$$$\mathrm{if}\:{z}=\mathrm{1}\wedge{x}=\frac{\mathrm{1}}{\mathrm{2}}: \\ $$$${z}=\mathrm{1e}^{\mathrm{0i}} \\ $$$$\mathrm{z}^{{x}} =\left(\mathrm{1e}^{\mathrm{0i}} \right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}^{\mathrm{1}/\mathrm{2}} \mathrm{e}^{\mathrm{0i}/\mathrm{2}} =\mathrm{1e}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{how}\:\mathrm{would}\:\mathrm{you}\:\mathrm{get}\:−\mathrm{1}?\:^{\left(\ast\right)} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{mistake}\:\mathrm{comes}\:\mathrm{ftom}\:\mathrm{solving}\:\mathrm{equations} \\ $$$$\mathrm{where}\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:\mathrm{different}\:\mathrm{rule}. \\ $$$${x}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:{x}=\pm\mathrm{1} \\ $$$$\mathrm{because}\:\mathrm{here}\:\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{all}\:\mathrm{values} \\ $$$$\mathrm{of}\:{x}\:\mathrm{which}\:\mathrm{give}\:\mathrm{1}\:\mathrm{if}\:\mathrm{we}\:\mathrm{square}\:{x} \\ $$$$\left(+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$\left(\ast\right) \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{exception}\:\mathrm{is}\:\mathrm{being}\:\mathrm{made}\:\mathrm{for} \\ $$$$\mathrm{geometric}\:\mathrm{problems}\:\mathrm{to}\:\mathrm{stay}\:\mathrm{in}\:\mathbb{R},\:{ignoring} \\ $$$$\mathrm{numbers}\:\in\mathbb{C}\:\left(\mathrm{because}\:\mathrm{they}\:\mathrm{had}\:\mathrm{not}\:\mathrm{been}\right. \\ $$$$\left.\mathrm{invented}\:\mathrm{yet}\:\mathrm{in}\:\mathrm{the}\:\mathrm{age}\:\mathrm{of}\:\mathrm{geometry}\right): \\ $$$$\sqrt[{\mathrm{3}}]{−\mathrm{8}}=\left(−\mathrm{8}\right)^{\mathrm{1}/\mathrm{3}} =−\mathrm{2} \\ $$$$\mathrm{we}\:\mathrm{artificially}\:\mathrm{take}\:\mathrm{the}\:\mathrm{root}\:\in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{for}\:{x}\in\mathbb{C}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(−\mathrm{8}\right)^{\mathrm{1}/\mathrm{3}} =\left(\mathrm{8e}^{\mathrm{i}\pi} \right)^{\mathrm{1}/\mathrm{3}} =\mathrm{8}^{\mathrm{1}/\mathrm{3}} \mathrm{e}^{\mathrm{i}\pi/\mathrm{3}} =\mathrm{2e}^{\mathrm{i}\pi/\mathrm{3}} \notin\mathbb{R} \\ $$

Commented by mr W last updated on 21/Mar/25

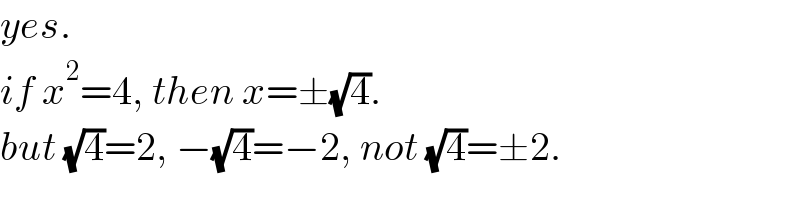
yes. if x^2 =4, then x=±(√4). but (√4)=2, −(√4)=−2, not (√4)=±2.

$${yes}. \\ $$$${if}\:{x}^{\mathrm{2}} =\mathrm{4},\:{then}\:{x}=\pm\sqrt{\mathrm{4}}. \\ $$$${but}\:\sqrt{\mathrm{4}}=\mathrm{2},\:−\sqrt{\mathrm{4}}=−\mathrm{2},\:{not}\:\sqrt{\mathrm{4}}=\pm\mathrm{2}. \\ $$

Commented by Marzuk last updated on 21/Mar/25

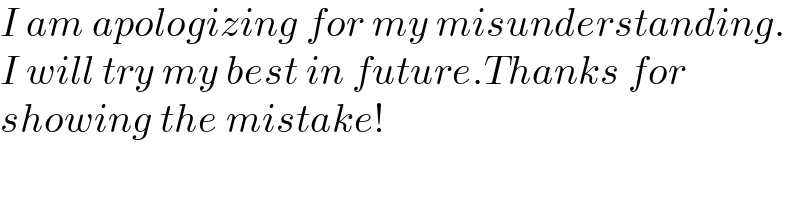
I am apologizing for my misunderstanding. I will try my best in future.Thanks for showing the mistake!

$${I}\:{am}\:{apologizing}\:{for}\:{my}\:{misunderstanding}. \\ $$$${I}\:{will}\:{try}\:{my}\:{best}\:{in}\:{future}.{Thanks}\:{for} \\ $$$${showing}\:{the}\:{mistake}! \\ $$

Commented by Ghisom last updated on 21/Mar/25

no need to apologize you live − you learn I might be a fraction of a step further than you are but still looking at the countless backs of those before me

$$\mathrm{no}\:\mathrm{need}\:\mathrm{to}\:\mathrm{apologize} \\ $$$$\mathrm{you}\:\mathrm{live}\:−\:\mathrm{you}\:\mathrm{learn} \\ $$$$\mathrm{I}\:\mathrm{might}\:\mathrm{be}\:\mathrm{a}\:\mathrm{fraction}\:\mathrm{of}\:\mathrm{a}\:\mathrm{step}\:\mathrm{further}\:\mathrm{than} \\ $$$$\mathrm{you}\:\mathrm{are}\:\mathrm{but}\:\mathrm{still}\:\mathrm{looking}\:\mathrm{at}\:\mathrm{the}\:\mathrm{countless} \\ $$$$\mathrm{backs}\:\mathrm{of}\:\mathrm{those}\:\mathrm{before}\:\mathrm{me} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com