Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 179773 by Acem last updated on 02/Nov/22

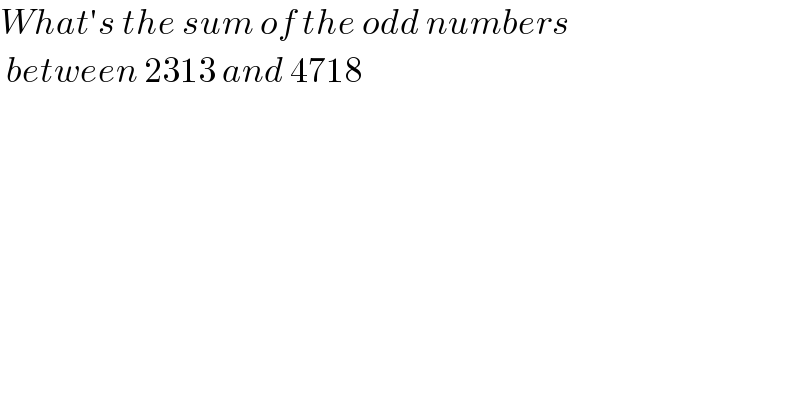
What′s the sum of the odd numbers between 2313 and 4718

$${What}'{s}\:{the}\:{sum}\:{of}\:{the}\:{odd}\:{numbers} \\ $$$$\:{between}\:\mathrm{2313}\:{and}\:\mathrm{4718} \\ $$

Commented by CElcedricjunior last updated on 05/Nov/22

calculons la somme des nombres comprises entre 2313 et 4718 ⇔2314+2315+......+4717 =(2313+1)+(2313+2)+......(2313+2404) =2313×2404+((2404×2405)/2) =2313×2404+1202×2405 =8.451.262 d′ou^� Σ_(k=2314) ^(4717) k=8.451.262

$$\boldsymbol{{calculons}}\:\boldsymbol{{la}}\:\boldsymbol{{somme}}\:\boldsymbol{{des}}\:\boldsymbol{{nombres}} \\ $$$$\boldsymbol{{comprises}}\:\boldsymbol{{entre}}\:\mathrm{2313}\:\boldsymbol{{et}}\:\mathrm{4718} \\ $$$$\Leftrightarrow\mathrm{2314}+\mathrm{2315}+......+\mathrm{4717} \\ $$$$=\left(\mathrm{2313}+\mathrm{1}\right)+\left(\mathrm{2313}+\mathrm{2}\right)+......\left(\mathrm{2313}+\mathrm{2404}\right) \\ $$$$=\mathrm{2313}×\mathrm{2404}+\frac{\mathrm{2404}×\mathrm{2405}}{\mathrm{2}} \\ $$$$=\mathrm{2313}×\mathrm{2404}+\mathrm{1202}×\mathrm{2405} \\ $$$$=\mathrm{8}.\mathrm{451}.\mathrm{262} \\ $$$${d}'\boldsymbol{{o}}\grave {\boldsymbol{{u}}}\:\underset{\boldsymbol{{k}}=\mathrm{2314}} {\overset{\mathrm{4717}} {\sum}}\boldsymbol{{k}}=\mathrm{8}.\mathrm{451}.\mathrm{262} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Nov/22

Sum of odd numbers between 2313 and 4718( exclusively) 2315+2317+...+4717 a=2315,l=4717, d=2, l=a_n =a+(n−1)d=2315+2(n−1)=4717 n=(4717−2315+2)/2=1202 determinant (((S_n =(n/2)(a+l)))) S_(1202) =((1202)/2)(2315+4717)=4226232

$${Sum}\:{of}\:{odd}\:{numbers} \\ $$$$\:{between}\:\mathrm{2313}\:{and}\:\mathrm{4718}\left(\:{exclusively}\right) \\ $$$$\mathrm{2315}+\mathrm{2317}+...+\mathrm{4717} \\ $$$${a}=\mathrm{2315},{l}=\mathrm{4717},\:{d}=\mathrm{2}, \\ $$$$\:{l}={a}_{{n}} ={a}+\left({n}−\mathrm{1}\right){d}=\mathrm{2315}+\mathrm{2}\left({n}−\mathrm{1}\right)=\mathrm{4717} \\ $$$${n}=\left(\mathrm{4717}−\mathrm{2315}+\mathrm{2}\right)/\mathrm{2}=\mathrm{1202} \\ $$$$\begin{array}{|c|}{{S}_{{n}} =\frac{{n}}{\mathrm{2}}\left({a}+{l}\right)}\\\hline\end{array} \\ $$$${S}_{\mathrm{1202}} =\frac{\mathrm{1202}}{\mathrm{2}}\left(\mathrm{2315}+\mathrm{4717}\right)=\mathrm{4226232} \\ $$

Commented by Acem last updated on 02/Nov/22

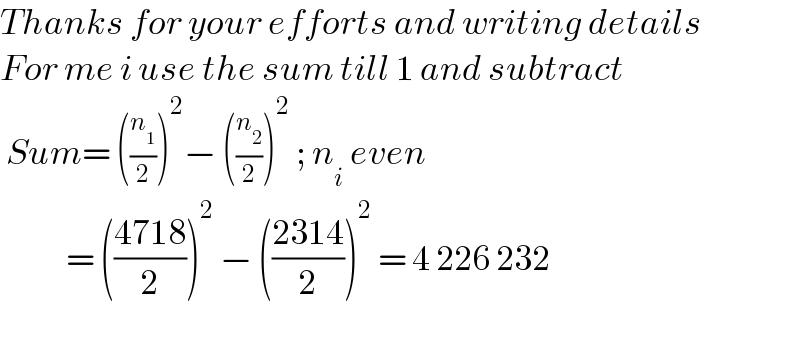
Thanks for your efforts and writing details For me i use the sum till 1 and subtract Sum= ((n_1 /2))^2 − ((n_2 /2))^2 ; n_i even = (((4718)/2))^2 − (((2314)/2))^2 = 4 226 232

$${Thanks}\:{for}\:{your}\:{efforts}\:{and}\:{writing}\:{details} \\ $$$${For}\:{me}\:{i}\:{use}\:{the}\:{sum}\:{till}\:\mathrm{1}\:{and}\:{subtract} \\ $$$$\:{Sum}=\:\left(\frac{{n}_{\mathrm{1}} }{\mathrm{2}}\right)^{\mathrm{2}} −\:\left(\frac{{n}_{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} \:;\:{n}_{{i}} \:{even} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\left(\frac{\mathrm{4718}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\:\left(\frac{\mathrm{2314}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\mathrm{4}\:\mathrm{226}\:\mathrm{232} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com