
Question Number 114401 by bemath last updated on 19/Sep/20
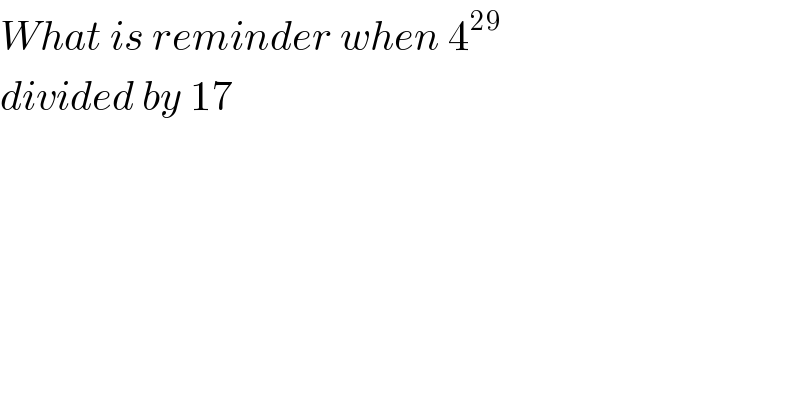
$${What}\:{is}\:{reminder}\:{when}\:\mathrm{4}^{\mathrm{29}} \\ $$$${divided}\:{by}\:\mathrm{17} \\ $$
Answered by bobhans last updated on 19/Sep/20
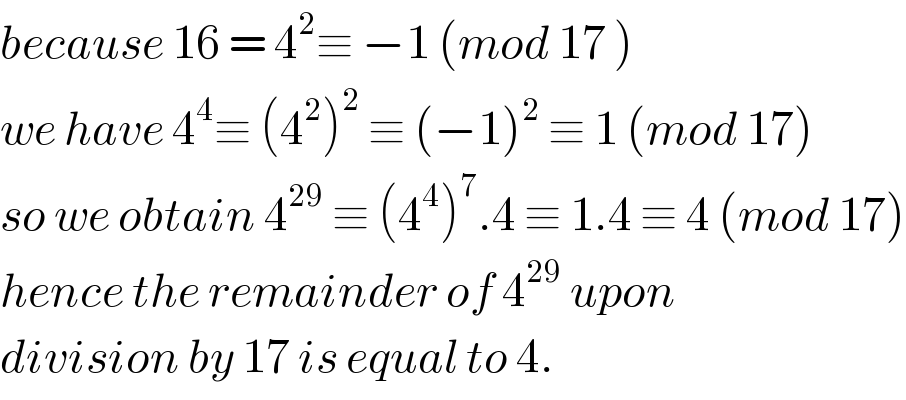
$${because}\:\mathrm{16}\:=\:\mathrm{4}^{\mathrm{2}} \equiv\:−\mathrm{1}\:\left({mod}\:\mathrm{17}\:\right) \\ $$$${we}\:{have}\:\mathrm{4}^{\mathrm{4}} \equiv\:\left(\mathrm{4}^{\mathrm{2}} \right)^{\mathrm{2}} \:\equiv\:\left(−\mathrm{1}\right)^{\mathrm{2}} \:\equiv\:\mathrm{1}\:\left({mod}\:\mathrm{17}\right) \\ $$$${so}\:{we}\:{obtain}\:\mathrm{4}^{\mathrm{29}} \:\equiv\:\left(\mathrm{4}^{\mathrm{4}} \right)^{\mathrm{7}} .\mathrm{4}\:\equiv\:\mathrm{1}.\mathrm{4}\:\equiv\:\mathrm{4}\:\left({mod}\:\mathrm{17}\right) \\ $$$${hence}\:{the}\:{remainder}\:{of}\:\mathrm{4}^{\mathrm{29}} \:{upon}\: \\ $$$${division}\:{by}\:\mathrm{17}\:{is}\:{equal}\:{to}\:\mathrm{4}. \\ $$
Commented by bemath last updated on 19/Sep/20

$${gave}\:{kudos}\:\checkmark\spadesuit \\ $$
