
Question Number 30429 by NECx last updated on 22/Feb/18

$${What}\:{are}\:{the}\:{conditions}\:{for}\:{using} \\ $$$${L}'{hospital}\:{rule}? \\ $$
Commented by prof Abdo imad last updated on 22/Feb/18
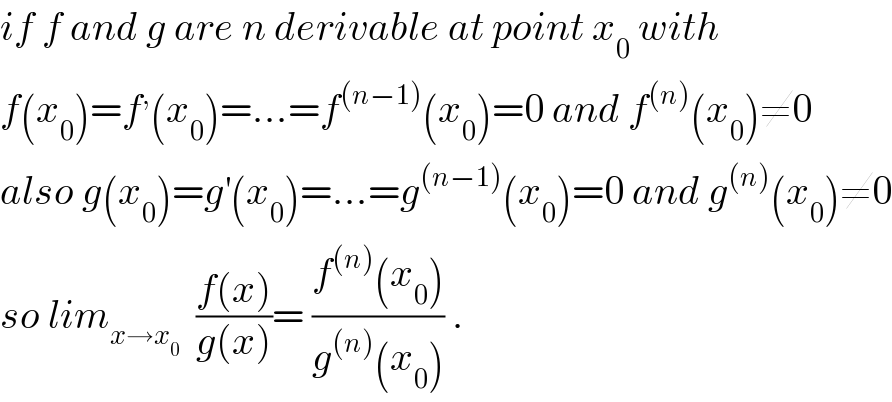
$${if}\:{f}\:{and}\:{g}\:{are}\:{n}\:{derivable}\:{at}\:{point}\:{x}_{\mathrm{0}} \:{with} \\ $$$${f}\left({x}_{\mathrm{0}} \right)={f}^{,} \left({x}_{\mathrm{0}} \right)=...={f}^{\left({n}−\mathrm{1}\right)} \left({x}_{\mathrm{0}} \right)=\mathrm{0}\:{and}\:{f}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)\neq\mathrm{0} \\ $$$${also}\:{g}\left({x}_{\mathrm{0}} \right)={g}^{'} \left({x}_{\mathrm{0}} \right)=...={g}^{\left({n}−\mathrm{1}\right)} \left({x}_{\mathrm{0}} \right)=\mathrm{0}\:{and}\:{g}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)\neq\mathrm{0} \\ $$$${so}\:{lim}_{{x}\rightarrow{x}_{\mathrm{0}} } \:\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\:\frac{{f}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)}{{g}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)}\:. \\ $$
