
Question Number 101510 by bemath last updated on 03/Jul/20
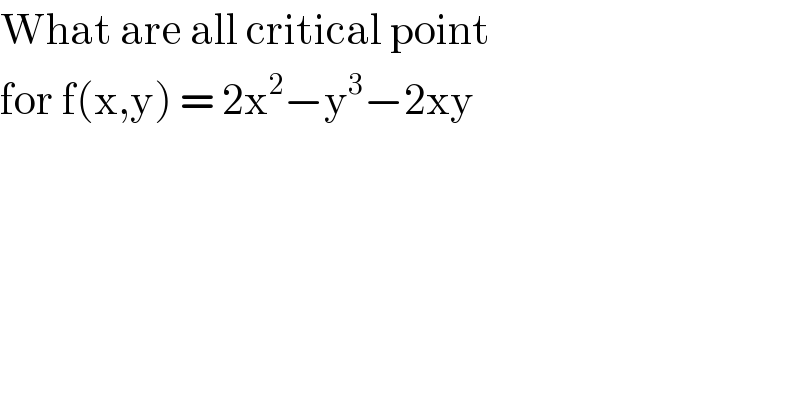
$$\mathrm{What}\:\mathrm{are}\:\mathrm{all}\:\mathrm{critical}\:\mathrm{point} \\ $$$$\mathrm{for}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{2x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{3}} −\mathrm{2xy} \\ $$
Commented by bramlex last updated on 03/Jul/20
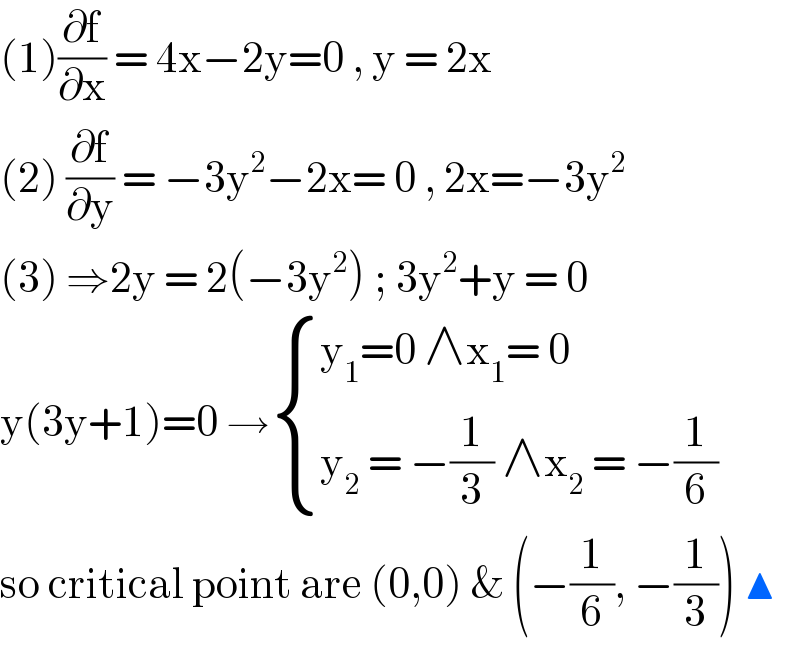
$$\left(\mathrm{1}\right)\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\:=\:\mathrm{4x}−\mathrm{2y}=\mathrm{0}\:,\:\mathrm{y}\:=\:\mathrm{2x} \\ $$$$\left(\mathrm{2}\right)\:\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\:=\:−\mathrm{3y}^{\mathrm{2}} −\mathrm{2x}=\:\mathrm{0}\:,\:\mathrm{2x}=−\mathrm{3y}^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\Rightarrow\mathrm{2y}\:=\:\mathrm{2}\left(−\mathrm{3y}^{\mathrm{2}} \right)\:;\:\mathrm{3y}^{\mathrm{2}} +\mathrm{y}\:=\:\mathrm{0} \\ $$$$\mathrm{y}\left(\mathrm{3y}+\mathrm{1}\right)=\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{y}_{\mathrm{1}} =\mathrm{0}\:\wedge\mathrm{x}_{\mathrm{1}} =\:\mathrm{0}}\\{\mathrm{y}_{\mathrm{2}} \:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:\wedge\mathrm{x}_{\mathrm{2}} \:=\:−\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$$$\mathrm{so}\:\mathrm{critical}\:\mathrm{point}\:\mathrm{are}\:\left(\mathrm{0},\mathrm{0}\right)\:\&\:\left(−\frac{\mathrm{1}}{\mathrm{6}},\:−\frac{\mathrm{1}}{\mathrm{3}}\right)\:\blacktriangle \\ $$
