
Question Number 197640 by Mastermind last updated on 25/Sep/23

$${Water}\:{is}\:{leaking}\:{from}\:{a}\:{hemispheric} \\ $$$${bowl}\:{of}\:{radius}\:\mathrm{20}{cm}\:{at}\:{the}\:{rate}\:{of}\: \\ $$$$\mathrm{0}.\mathrm{5}{cm}^{\mathrm{3}} /{s}.\:{Find}\:{the}\:{rate}\:{at}\:{which}\:{surface} \\ $$$${area}\:{of}\:{the}\:{water}\:{decreasing}\:{when}\:{the} \\ $$$${water}\:{level}\:{is}\:{halfway}\:{from}\:{the}\:{top}. \\ $$$$ \\ $$$${Thank}\:{you} \\ $$
Answered by mr W last updated on 25/Sep/23
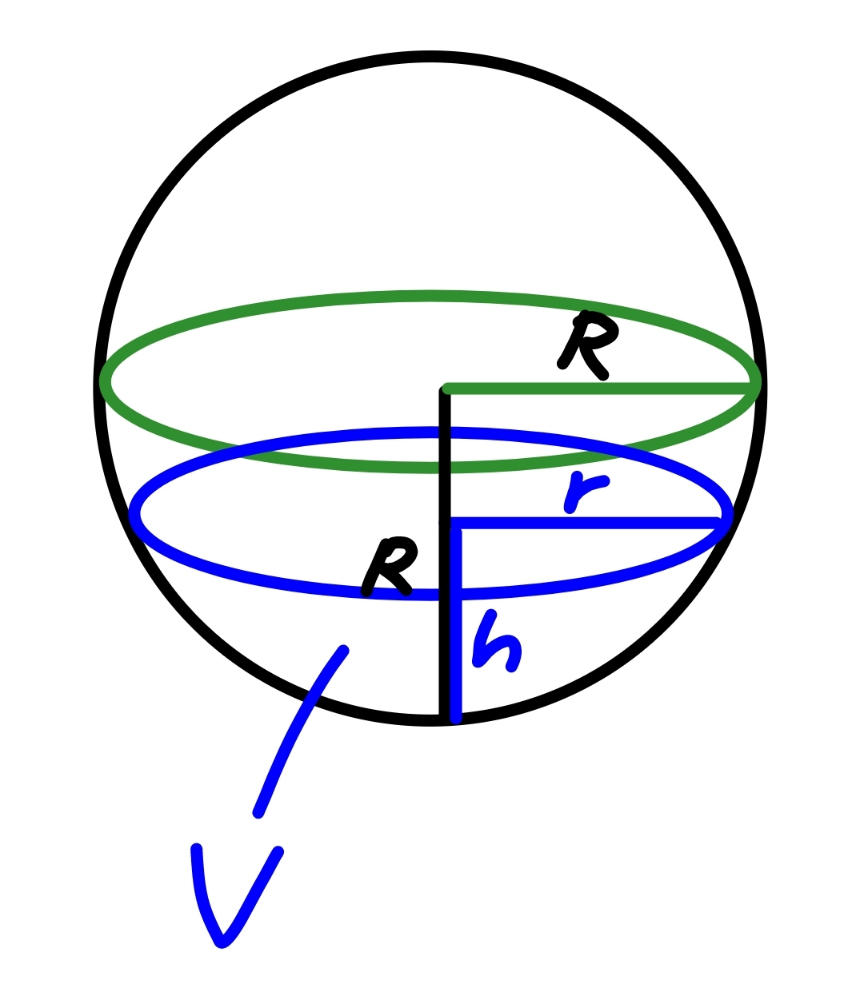
Commented by mr W last updated on 25/Sep/23
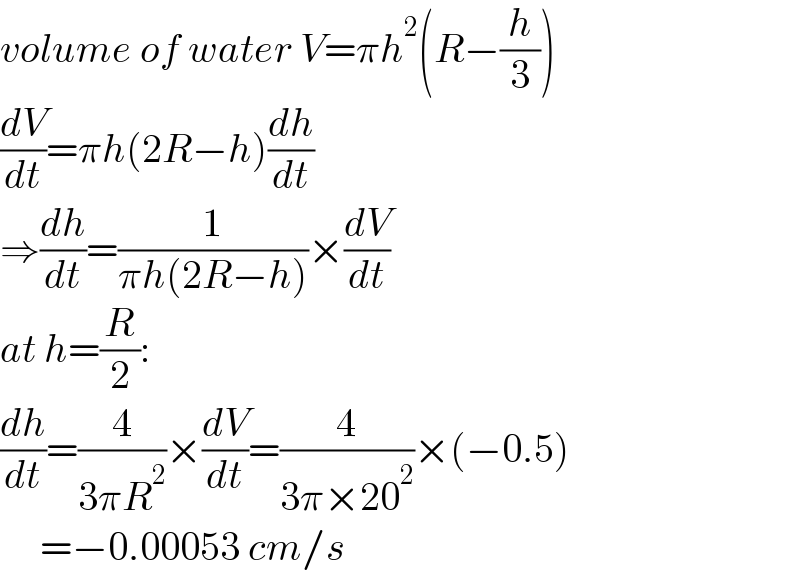
$${volume}\:{of}\:{water}\:{V}=\pi{h}^{\mathrm{2}} \left({R}−\frac{{h}}{\mathrm{3}}\right) \\ $$$$\frac{{dV}}{{dt}}=\pi{h}\left(\mathrm{2}{R}−{h}\right)\frac{{dh}}{{dt}} \\ $$$$\Rightarrow\frac{{dh}}{{dt}}=\frac{\mathrm{1}}{\pi{h}\left(\mathrm{2}{R}−{h}\right)}×\frac{{dV}}{{dt}} \\ $$$${at}\:{h}=\frac{{R}}{\mathrm{2}}: \\ $$$$\frac{{dh}}{{dt}}=\frac{\mathrm{4}}{\mathrm{3}\pi{R}^{\mathrm{2}} }×\frac{{dV}}{{dt}}=\frac{\mathrm{4}}{\mathrm{3}\pi×\mathrm{20}^{\mathrm{2}} }×\left(−\mathrm{0}.\mathrm{5}\right) \\ $$$$\:\:\:\:\:=−\mathrm{0}.\mathrm{00053}\:{cm}/{s} \\ $$
Commented by Mastermind last updated on 25/Sep/23
$${Thank}\:{you}\:{so}\:{much} \\ $$
