
Question Number 191735 by Spillover last updated on 29/Apr/23
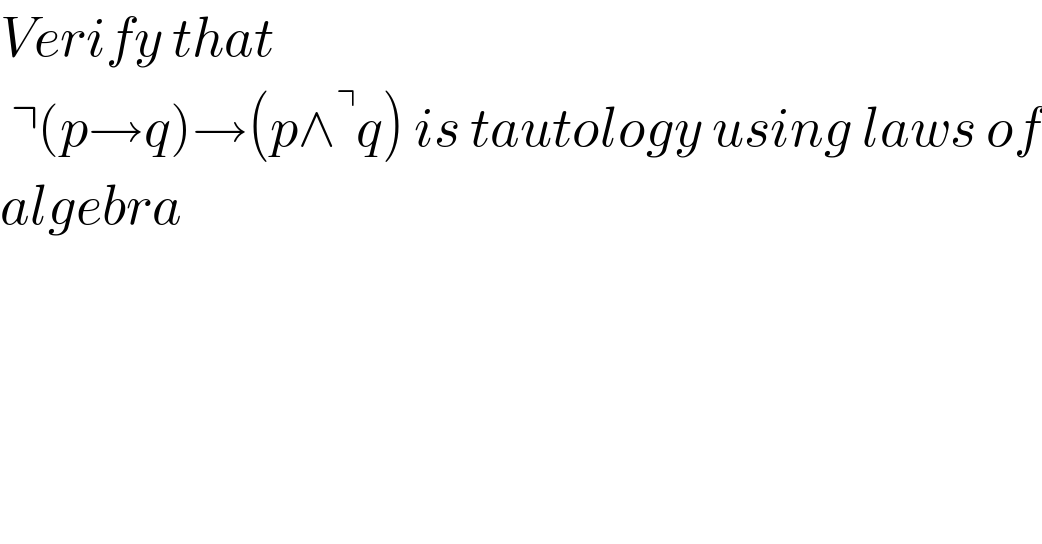
$${Verify}\:{that} \\ $$$$\:\urcorner\left({p}\rightarrow{q}\right)\rightarrow\left({p}\wedge^{\urcorner} {q}\right)\:{is}\:{tautology}\:{using}\:{laws}\:{of} \\ $$$${algebra} \\ $$
Answered by manxsol last updated on 30/Apr/23
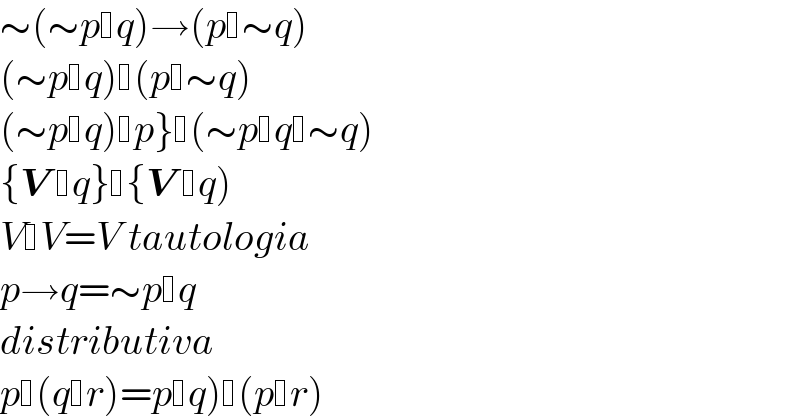
$$\sim\left(\sim{p} {q}\right)\rightarrow\left({p} \sim{q}\right) \\ $$$$\left(\sim{p} {q}\right) \left({p} \sim{q}\right) \\ $$$$\left.\left(\sim{p} {q}\right) {p}\right\} \left(\sim{p} {q} \sim{q}\right) \\ $$$$\left\{\boldsymbol{{V}}\: {q}\right\} \left\{\boldsymbol{{V}}\: {q}\right) \\ $$$${V} {V}={V}\:{tautologia} \\ $$$${p}\rightarrow{q}=\sim{p} {q} \\ $$$${distributiva} \\ $$$$\left.{p} \left({q} {r}\right)={p} {q}\right) \left({p} {r}\right) \\ $$
Answered by aba last updated on 30/Apr/23
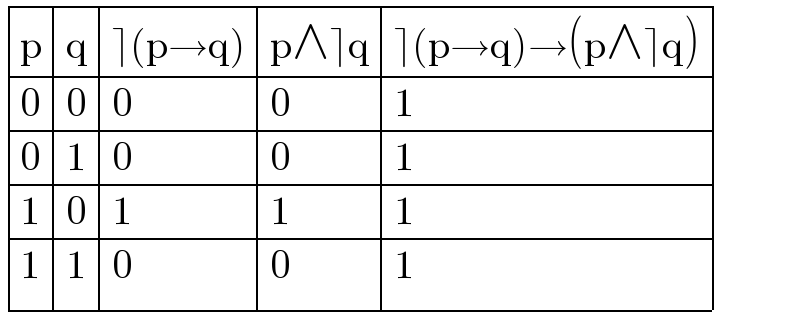
$$\begin{array}{|c|c|c|c|c|}{\mathrm{p}}&\hline{\mathrm{q}}&\hline{\rceil\left(\mathrm{p}\rightarrow\mathrm{q}\right)}&\hline{\mathrm{p}\wedge\rceil\mathrm{q}}&\hline{\rceil\left(\mathrm{p}\rightarrow\mathrm{q}\right)\rightarrow\left(\mathrm{p}\wedge\rceil\mathrm{q}\right)}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\\hline\end{array} \\ $$
Commented by Spillover last updated on 30/Apr/23
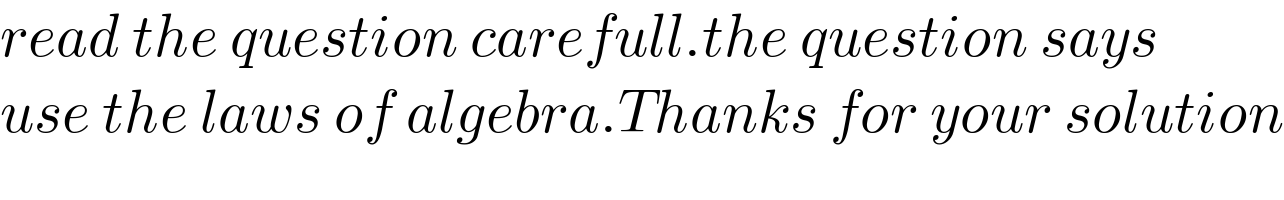
$${read}\:{the}\:{question}\:{carefull}.{the}\:{question}\:{says} \\ $$$${use}\:{the}\:{laws}\:{of}\:{algebra}.{Thanks}\:{for}\:{your}\:{solution} \\ $$
Commented by aba last updated on 30/Apr/23

$$\mathrm{i}\:\mathrm{know} \\ $$
Answered by Spillover last updated on 30/Apr/23
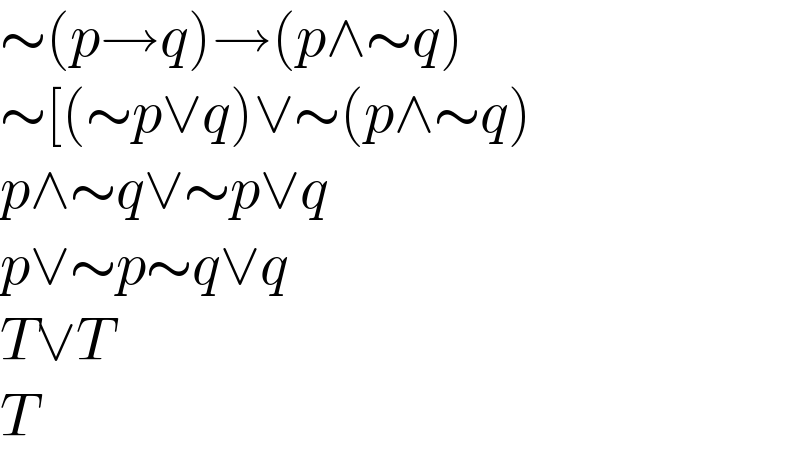
$$\sim\left({p}\rightarrow{q}\right)\rightarrow\left({p}\wedge\sim{q}\right) \\ $$$$\sim\left[\left(\sim{p}\vee{q}\right)\vee\sim\left({p}\wedge\sim{q}\right)\:\:\right. \\ $$$${p}\wedge\sim{q}\vee\sim{p}\vee{q} \\ $$$${p}\vee\sim{p}\sim{q}\vee{q} \\ $$$${T}\vee{T} \\ $$$${T} \\ $$
