
Question Number 216351 by issac last updated on 05/Feb/25
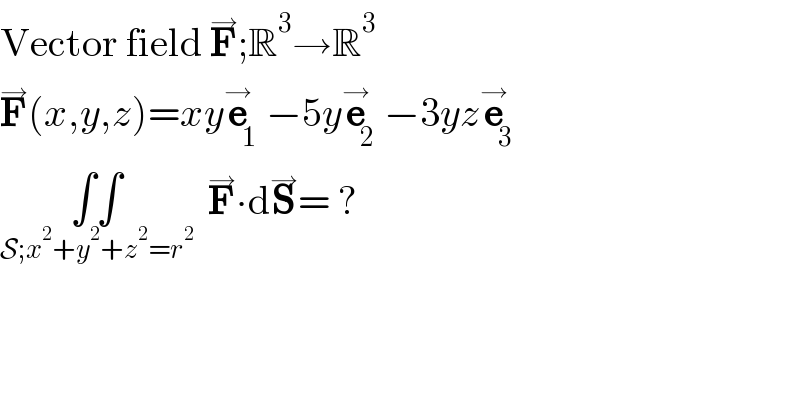
$$\mathrm{Vector}\:\mathrm{field}\:\overset{\rightarrow} {\boldsymbol{\mathrm{F}}};\mathbb{R}^{\mathrm{3}} \rightarrow\mathbb{R}^{\mathrm{3}} \\ $$$$\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}\left({x},{y},{z}\right)={xy}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{1}} −\mathrm{5}{y}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{2}} −\mathrm{3}{yz}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{3}} \\ $$$$\underset{\mathcal{S};{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={r}^{\mathrm{2}} } {\int\int}\:\:\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}\centerdot\mathrm{d}\overset{\rightarrow} {\boldsymbol{\mathrm{S}}}=\:? \\ $$
Answered by MrGaster last updated on 06/Feb/25
![▽∙F^→ =(∂/∂x)(∂y)+(∂/∂y)(−5y)+(∂/∂z)(−3yz) =y−5−3y=−2y−5 ∫∫∫_V (−2y−5)dV x=r sin θ cos φ,y=r sinθ sin φ,z=r cos θ dV=r^2 sinθ dr dθ dφ 0≤r≤r,0≤θ≤π,0≤φ≤2π ∫∫∫_V (−2y−5)dV=∫_0 ^r ∫_0 ^π ∫_0 ^(2π) (−2r sinθ φ−5)r^2 sinθ dφ dθ dr =∫_(0 ) ^r ∫_(0 ) ^π [−2r^3 sin^2 θ∫_0 ^(2π) sinφdφ−5r^2 sinθ∫_0 ^(2π) dφ]dθ dr ∫_0 ^r ∫_0 ^π [0−10πr^2 sinθ]dθ dr =−10π∫_0 ^r ∫_0 ^π r^2 sinθ dθ dr =−10π∫_0 ^r ∫_0 ^π [−r^2 cosθ]_0 ^π dr =−10π∫_0 ^r 2r^2 dr =−20π[(r^3 /3)]_0 ^r = determinant (((−((20πr^3 )/3))))](Q216375.png)
$$\bigtriangledown\centerdot\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}=\frac{\partial}{\partial{x}}\left(\partial{y}\right)+\frac{\partial}{\partial{y}}\left(−\mathrm{5}{y}\right)+\frac{\partial}{\partial{z}}\left(−\mathrm{3}{yz}\right) \\ $$$$={y}−\mathrm{5}−\mathrm{3}{y}=−\mathrm{2}{y}−\mathrm{5} \\ $$$$\int\int\int_{{V}} \left(−\mathrm{2}{y}−\mathrm{5}\right){dV} \\ $$$${x}={r}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\phi,{y}={r}\:\mathrm{sin}\theta\:\mathrm{sin}\:\phi,{z}={r}\:\mathrm{cos}\:\theta \\ $$$${dV}={r}^{\mathrm{2}} \mathrm{sin}\theta\:{dr}\:{d}\theta\:{d}\phi \\ $$$$\mathrm{0}\leq{r}\leq{r},\mathrm{0}\leq\theta\leq\pi,\mathrm{0}\leq\phi\leq\mathrm{2}\pi \\ $$$$\int\int\int_{{V}} \left(−\mathrm{2}{y}−\mathrm{5}\right){dV}=\int_{\mathrm{0}} ^{{r}} \int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(−\mathrm{2}{r}\:\mathrm{sin}\theta\:\phi−\mathrm{5}\right){r}^{\mathrm{2}} \:\mathrm{sin}\theta\:{d}\phi\:{d}\theta\:{dr} \\ $$$$=\int_{\mathrm{0}\:} ^{{r}} \int_{\mathrm{0}\:} ^{\pi} \left[−\mathrm{2}{r}^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \theta\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{sin}\phi{d}\phi−\mathrm{5r}^{\mathrm{2}} \mathrm{sin}\theta\int_{\mathrm{0}} ^{\mathrm{2}\pi} {d}\phi\right]{d}\theta\:{dr} \\ $$$$\int_{\mathrm{0}} ^{{r}} \int_{\mathrm{0}} ^{\pi} \left[\mathrm{0}−\mathrm{10}\pi{r}^{\mathrm{2}} \mathrm{sin}\theta\right]{d}\theta\:{dr} \\ $$$$=−\mathrm{10}\pi\int_{\mathrm{0}} ^{{r}} \int_{\mathrm{0}} ^{\pi} {r}^{\mathrm{2}} \mathrm{sin}\theta\:{d}\theta\:{dr} \\ $$$$=−\mathrm{10}\pi\int_{\mathrm{0}} ^{{r}} \int_{\mathrm{0}} ^{\pi} \left[−{r}^{\mathrm{2}} \mathrm{cos}\theta\right]_{\mathrm{0}} ^{\pi} {dr} \\ $$$$=−\mathrm{10}\pi\int_{\mathrm{0}} ^{{r}} \mathrm{2}{r}^{\mathrm{2}} {dr} \\ $$$$=−\mathrm{20}\pi\left[\frac{{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{{r}} \\ $$$$=\begin{array}{|c|}{−\frac{\mathrm{20}\pi{r}^{\mathrm{3}} }{\mathrm{3}}}\\\hline\end{array} \\ $$
Commented by issac last updated on 06/Feb/25
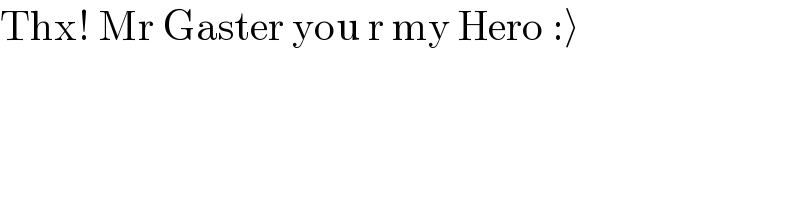
$$\mathrm{Thx}!\:\mathrm{Mr}\:\mathrm{Gaster}\:\mathrm{you}\:\mathrm{r}\:\mathrm{my}\:\mathrm{Hero}\::\rangle \\ $$
