Question and Answers Forum

Vector CalculusQuestion and Answers: Page 1

Question Number 222943 Answers: 4 Comments: 0

11. If (√5) = 2.236 and (√(10)) = 3.162 then the value of ((15)/( (√(10))+(√(20))+(√(40))−(√5)−(√(80)))) is (a) 5.398 (b) 4.398 (c) 3.398 (d) 6.398 12. If x=(((√3)+1)/3) then x^3 +(1/(x^3 ))=? (a) ((28(√3) +15)/8) (b) ((28(√3)−15)/8) (c) ((27(√3)−35)/4) (d) ((27(√3)+35)/4) 13. Simplify ((x^4 ((x^3_ ((x^2 (√x)))^(1/3) ))^(1/4) ))^(1/5) (a) x^((23)/(24)) (b) x^((23)/6) (c) x^(5/6) (d) x^((119)/(120)) 14.

Question Number 216698 Answers: 2 Comments: 0

lim_(x→+∞) ^3 (√(x+1)) −^3 (√x) =^? 0

$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\:−^{\mathrm{3}} \sqrt{{x}}\:\overset{?} {=}\:\mathrm{0} \\ $$

Question Number 213045 Answers: 1 Comments: 0

a^⇀ ,b^⇀ ls the unit vector,∣a^⇀ +b^⇀ ∣=1 ask ∣a^⇀ −b^⇀ ∣?

$$\overset{\rightharpoonup} {{a}},\overset{\rightharpoonup} {{b}ls}\:{the}\:{unit}\:{vector},\mid\overset{\rightharpoonup} {{a}}+\overset{\rightharpoonup} {{b}}\mid=\mathrm{1} \\ $$$${ask}\:\mid\overset{\rightharpoonup} {{a}}−\overset{\rightharpoonup} {{b}}\mid? \\ $$

Question Number 212616 Answers: 0 Comments: 1

if f(x)=^a x=x^x^x^⋰^x (there are a x′s;a∈N and a≠0) ∫f(x)dx=?

$$ \\ $$$$ \\ $$$${if}\:\:\mathrm{f}\left(\mathrm{x}\right)=\:^{{a}} {x}={x}^{{x}^{{x}^{\iddots^{{x}} } } } \left({there}\:{are}\:{a}\:{x}'{s};{a}\in\mathbb{N}\:{and}\:{a}\neq\mathrm{0}\right) \\ $$$$\int{f}\left({x}\right){dx}=? \\ $$

Question Number 210554 Answers: 1 Comments: 0

Question Number 209888 Answers: 0 Comments: 0

n_0 =((Z^2 .p.(1−p))/C^(2m) )

$${n}_{\mathrm{0}} =\frac{{Z}^{\mathrm{2}} .{p}.\left(\mathrm{1}−{p}\right)}{{C}^{\mathrm{2}{m}} } \\ $$

Question Number 207712 Answers: 1 Comments: 0

Question Number 205673 Answers: 0 Comments: 0

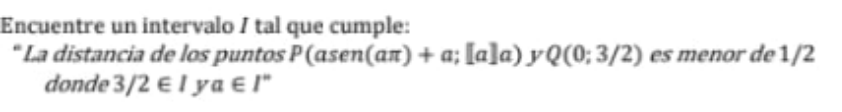
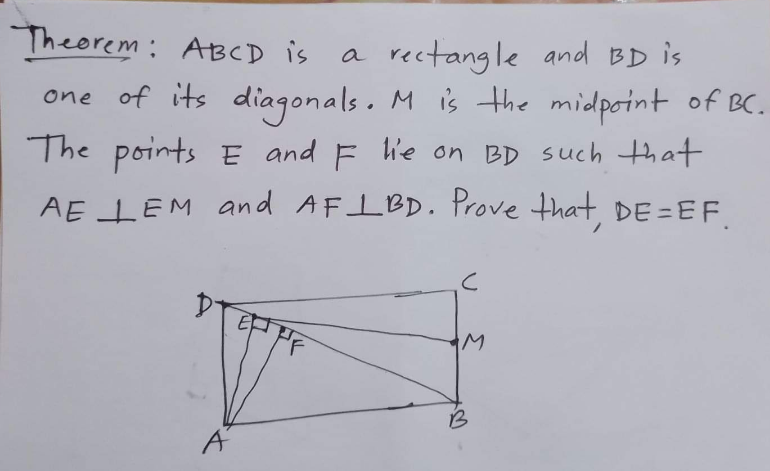
Question Number 204273 Answers: 1 Comments: 0

f(x)=(1/((x−1)^(ln((2/4))) )) Domain f(x) =?

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{4}}\right)} } \\ $$$$\mathrm{Domain}\:\mathrm{f}\left(\mathrm{x}\right)\:=? \\ $$

Question Number 203900 Answers: 0 Comments: 0

Let A ∈ R^(N×N) be a symmetric positive definite matrix and b ∈ R^N a vector. If x ∈ R^N , evaluate the integral Z(A,b) = ∫e^(−(1/2)x^T Ax + b^T x) dx as a function of A and b.

$${Let}\:{A}\:\in\:{R}^{{N}×{N}} \:{be}\:{a}\:{symmetric}\:{positive} \\ $$$${definite}\:{matrix}\:{and}\:{b}\:\in\:{R}^{{N}} \:{a}\:{vector}. \\ $$$${If}\:{x}\:\in\:{R}^{{N}} ,\:{evaluate}\:{the}\:{integral} \\ $$$${Z}\left({A},{b}\right)\:=\:\int{e}^{−\frac{\mathrm{1}}{\mathrm{2}}{x}^{{T}} {Ax}\:+\:{b}^{{T}} {x}} {dx}\:{as}\:{a}\:{function} \\ $$$${of}\:{A}\:{and}\:{b}. \\ $$

Question Number 201947 Answers: 1 Comments: 0

Question Number 201144 Answers: 2 Comments: 0

(((14)/(15)))^6 ×(((45)/(28)))^6 =

$$\left(\frac{\mathrm{14}}{\mathrm{15}}\right)^{\mathrm{6}} ×\left(\frac{\mathrm{45}}{\mathrm{28}}\right)^{\mathrm{6}} = \\ $$

Question Number 200929 Answers: 0 Comments: 2

A ball lies on the function z=xy at the point (1,2,2). Find the point in the xy−plane where the ball will touch it. Calculus 2 problem.

$$\mathrm{A}\:\mathrm{ball}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{the}\:\mathrm{function}\:{z}={xy}\:\mathrm{at} \\ $$$$\mathrm{the}\:\mathrm{point}\:\left(\mathrm{1},\mathrm{2},\mathrm{2}\right).\:\mathrm{Find}\:\mathrm{the}\:\mathrm{point}\:\mathrm{in} \\ $$$$\mathrm{the}\:{xy}−\mathrm{plane}\:\mathrm{where}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{will} \\ $$$$\mathrm{touch}\:\mathrm{it}. \\ $$$$\mathrm{Calculus}\:\mathrm{2}\:\mathrm{problem}. \\ $$

Question Number 196918 Answers: 1 Comments: 0

Question Number 196412 Answers: 1 Comments: 1

Prove that ∫^( +∞) _( i) (cos2t+isin2t)e^(−t^2 ) dt= ((√π)/(2e))

$$\mathrm{Prove}\:\mathrm{that}\:\underset{\:{i}} {\int}^{\:+\infty} \left(\mathrm{cos2t}+\mathrm{isin2t}\right)\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}=\:\frac{\sqrt{\pi}}{\mathrm{2e}} \\ $$

Question Number 193204 Answers: 1 Comments: 0

Question Number 192024 Answers: 1 Comments: 0

Question Number 192023 Answers: 2 Comments: 0

Question Number 191104 Answers: 1 Comments: 0

Question Number 190006 Answers: 0 Comments: 0

Question Number 186323 Answers: 1 Comments: 1

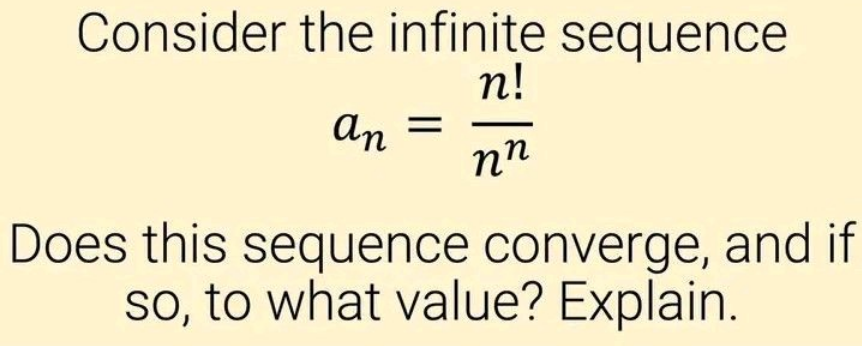
Question Number 185190 Answers: 0 Comments: 0

Question Number 184287 Answers: 2 Comments: 0

If the area enclosed between the curves y=x² and the line y = 2x is rotated round the x-axis through 4 right angles, find the volume of the solid generated

Question Number 182183 Answers: 1 Comments: 0

∫_0 ^( 1) e^a a^n da=? n≥1 n∈N

$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \boldsymbol{{e}}^{\boldsymbol{{a}}} \boldsymbol{{a}}^{\boldsymbol{{n}}} \boldsymbol{{da}}=?\:\:\:\:\:\:\:\:\boldsymbol{{n}}\geqslant\mathrm{1}\:\:\:\:\boldsymbol{{n}}\in\boldsymbol{{N}} \\ $$

Question Number 181678 Answers: 0 Comments: 0

$$ \\ $$

Question Number 179453 Answers: 1 Comments: 0

Pg 1 Pg 2 Pg 3 Pg 4 Pg 5 Pg 6

Contact: info@tinkutara.com