Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 129564 by bramlexs22 last updated on 16/Jan/21

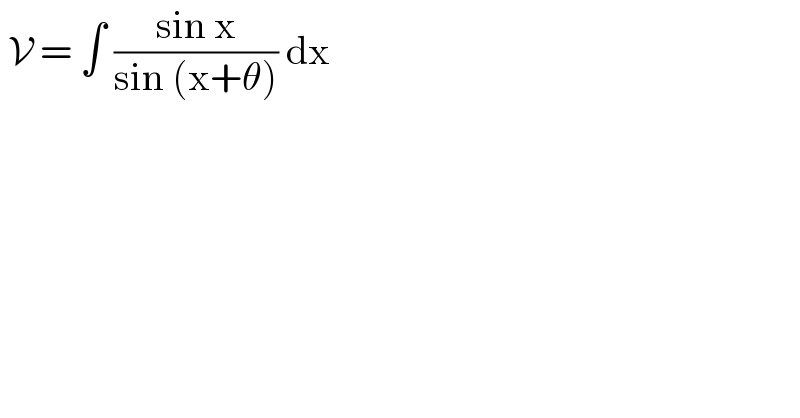
V = ∫ ((sin x)/(sin (x+θ))) dx

$$\:\mathcal{V}\:=\:\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\left(\mathrm{x}+\theta\right)}\:\mathrm{dx}\: \\ $$

Answered by Lordose last updated on 16/Jan/21

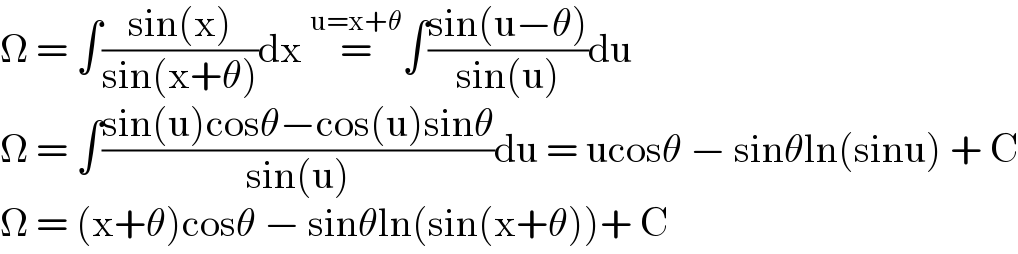
Ω = ∫((sin(x))/(sin(x+θ)))dx =^(u=x+θ) ∫((sin(u−θ))/(sin(u)))du Ω = ∫((sin(u)cosθ−cos(u)sinθ)/(sin(u)))du = ucosθ − sinθln(sinu) + C Ω = (x+θ)cosθ − sinθln(sin(x+θ))+ C

$$\Omega\:=\:\int\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{sin}\left(\mathrm{x}+\theta\right)}\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{x}+\theta} {=}\int\frac{\mathrm{sin}\left(\mathrm{u}−\theta\right)}{\mathrm{sin}\left(\mathrm{u}\right)}\mathrm{du} \\ $$$$\Omega\:=\:\int\frac{\mathrm{sin}\left(\mathrm{u}\right)\mathrm{cos}\theta−\mathrm{cos}\left(\mathrm{u}\right)\mathrm{sin}\theta}{\mathrm{sin}\left(\mathrm{u}\right)}\mathrm{du}\:=\:\mathrm{ucos}\theta\:−\:\mathrm{sin}\theta\mathrm{ln}\left(\mathrm{sinu}\right)\:+\:\mathrm{C} \\ $$$$\Omega\:=\:\left(\mathrm{x}+\theta\right)\mathrm{cos}\theta\:−\:\mathrm{sin}\theta\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}+\theta\right)\right)+\:\mathrm{C} \\ $$

Answered by liberty last updated on 16/Jan/21

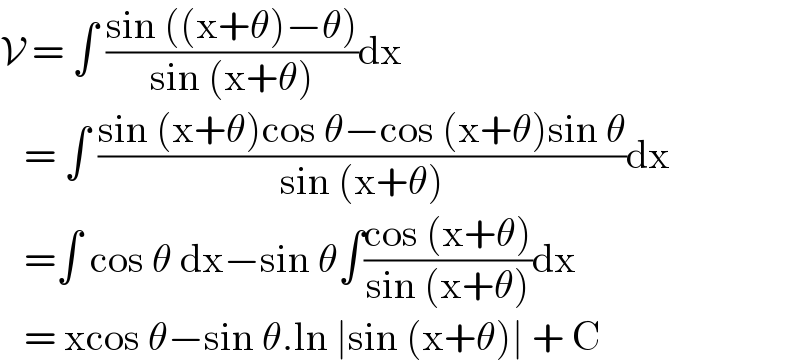
V = ∫ ((sin ((x+θ)−θ))/(sin (x+θ)))dx = ∫ ((sin (x+θ)cos θ−cos (x+θ)sin θ)/(sin (x+θ)))dx =∫ cos θ dx−sin θ∫((cos (x+θ))/(sin (x+θ)))dx = xcos θ−sin θ.ln ∣sin (x+θ)∣ + C

$$\mathcal{V}\:=\:\int\:\frac{\mathrm{sin}\:\left(\left(\mathrm{x}+\theta\right)−\theta\right)}{\mathrm{sin}\:\left(\mathrm{x}+\theta\right)}\mathrm{dx} \\ $$$$\:\:\:=\:\int\:\frac{\mathrm{sin}\:\left(\mathrm{x}+\theta\right)\mathrm{cos}\:\theta−\mathrm{cos}\:\left(\mathrm{x}+\theta\right)\mathrm{sin}\:\theta}{\mathrm{sin}\:\left(\mathrm{x}+\theta\right)}\mathrm{dx} \\ $$$$\:\:\:=\int\:\mathrm{cos}\:\theta\:\mathrm{dx}−\mathrm{sin}\:\theta\int\frac{\mathrm{cos}\:\left(\mathrm{x}+\theta\right)}{\mathrm{sin}\:\left(\mathrm{x}+\theta\right)}\mathrm{dx} \\ $$$$\:\:\:=\:\mathrm{xcos}\:\theta−\mathrm{sin}\:\theta.\mathrm{ln}\:\mid\mathrm{sin}\:\left(\mathrm{x}+\theta\right)\mid\:+\:\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com