
Question Number 128592 by BHOOPENDRA last updated on 09/Jan/21

$$\int\int\int_{{V}} \bigtriangledown×{F}\:{dV}\:{where}\:{F}=\left({x}+\mathrm{2}{y}\right)\hat {{i}}−\mathrm{3}{z}\hat {{j}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{x}\hat {{k}} \\ $$$${and}\:{V}\:{is}\:{the}\:{closed}\:{region}\:{in}\:{first}\:{octant} \\ $$$${by}\:{the}\:{plane}\:\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z}=\mathrm{4} \\ $$$$ \\ $$
Answered by Olaf last updated on 08/Jan/21
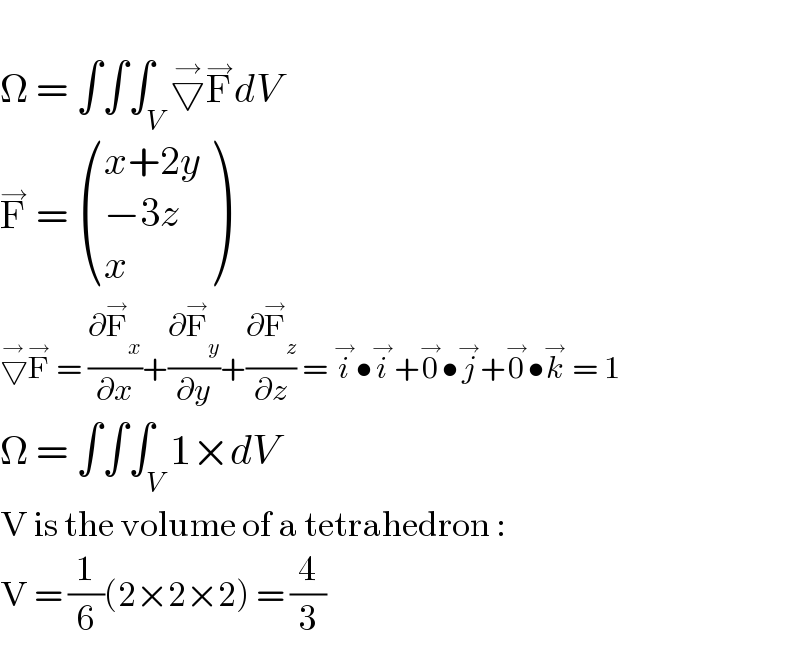
$$ \\ $$$$\Omega\:=\:\int\int\int_{{V}} \overset{\rightarrow} {\bigtriangledown}\overset{\rightarrow} {\mathrm{F}}{dV} \\ $$$$\overset{\rightarrow} {\mathrm{F}}\:=\:\begin{pmatrix}{{x}+\mathrm{2}{y}}\\{−\mathrm{3}{z}}\\{{x}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\bigtriangledown}\overset{\rightarrow} {\mathrm{F}}\:=\:\frac{\partial\overset{\rightarrow} {\mathrm{F}}_{{x}} }{\partial{x}}+\frac{\partial\overset{\rightarrow} {\mathrm{F}}_{{y}} }{\partial{y}}+\frac{\partial\overset{\rightarrow} {\mathrm{F}}_{{z}} }{\partial{z}}\:=\:\overset{\rightarrow} {{i}}\bullet\overset{\rightarrow} {{i}}+\overset{\rightarrow} {\mathrm{0}}\bullet\overset{\rightarrow} {{j}}+\overset{\rightarrow} {\mathrm{0}}\bullet\overset{\rightarrow} {{k}}\:=\:\mathrm{1} \\ $$$$\Omega\:=\:\int\int\int_{{V}} \mathrm{1}×{dV} \\ $$$$\mathrm{V}\:\mathrm{is}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{a}\:\mathrm{tetrahedron}\:: \\ $$$$\mathrm{V}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{2}×\mathrm{2}×\mathrm{2}\right)\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by BHOOPENDRA last updated on 09/Jan/21
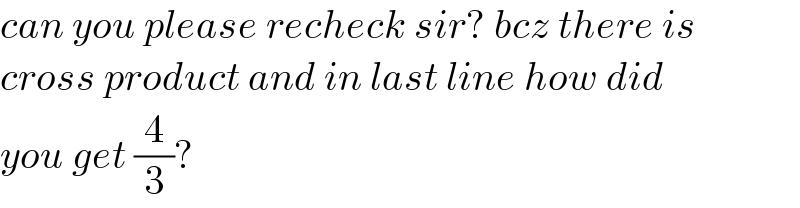
$${can}\:{you}\:{please}\:{recheck}\:{sir}?\:{bcz}\:{there}\:{is}\: \\ $$$${cross}\:{product}\:{and}\:{in}\:{last}\:{line}\:{how}\:{did}\: \\ $$$${you}\:{get}\:\frac{\mathrm{4}}{\mathrm{3}}? \\ $$
