
Question Number 122496 by benjo_mathlover last updated on 17/Nov/20
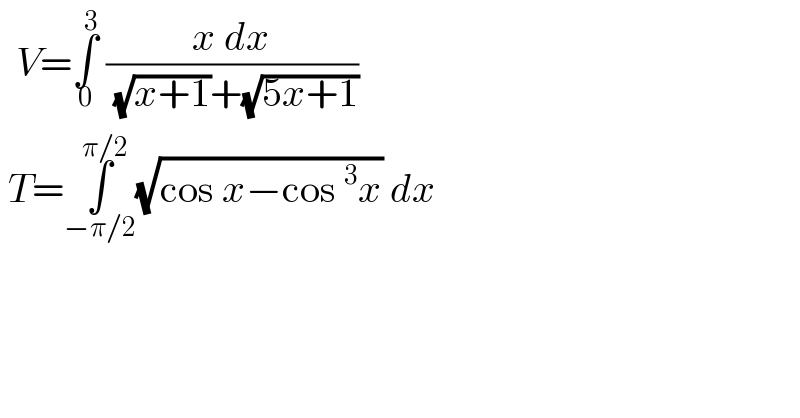
$$\:\:{V}=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{{x}\:{dx}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{\mathrm{5}{x}+\mathrm{1}}} \\ $$$$\:{T}=\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\mathrm{cos}\:{x}−\mathrm{cos}\:^{\mathrm{3}} {x}}\:{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 17/Nov/20
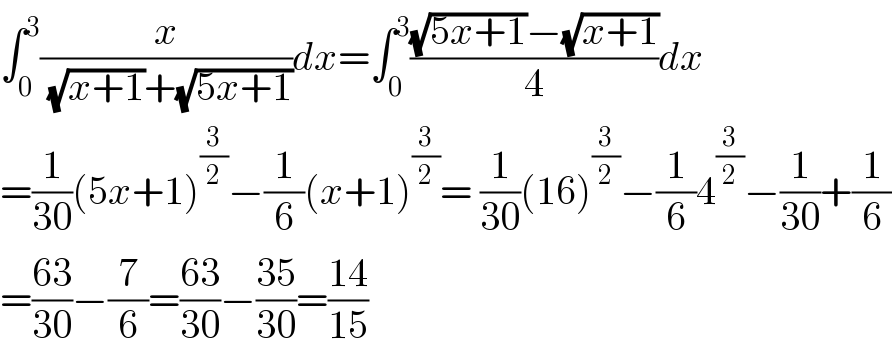
$$\int_{\mathrm{0}} ^{\mathrm{3}} \frac{{x}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{\mathrm{5}{x}+\mathrm{1}}}{dx}=\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\sqrt{\mathrm{5}{x}+\mathrm{1}}−\sqrt{{x}+\mathrm{1}}}{\mathrm{4}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{5}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{6}}\left({x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\:\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{16}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{6}}\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{63}}{\mathrm{30}}−\frac{\mathrm{7}}{\mathrm{6}}=\frac{\mathrm{63}}{\mathrm{30}}−\frac{\mathrm{35}}{\mathrm{30}}=\frac{\mathrm{14}}{\mathrm{15}} \\ $$
Answered by MJS_new last updated on 17/Nov/20
![∫_(−π/2) ^(π/2) (√(cos x −cos^3 x)) dx=∫_(−π/2) ^(π/2) (√((1−cos^2 x)cos x)) dx= =∫_(−π/2) ^(π/2) ∣sin x∣(√(cos x)) dx=2∫_0 ^(π/2) sin x (√(cos x)) dx= [t=cos x → dx=−(dt/(sin x))] =−2∫_1 ^0 (√t)dt=2∫_0 ^1 (√t)dt=2[(2/3)t^(3/2) ]_0 ^1 =(4/3)](Q122504.png)
$$\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\mathrm{cos}\:{x}\:−\mathrm{cos}^{\mathrm{3}} \:{x}}\:{dx}=\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}\right)\mathrm{cos}\:{x}}\:{dx}= \\ $$$$=\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\mid\mathrm{sin}\:{x}\mid\sqrt{\mathrm{cos}\:{x}}\:{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{sin}\:{x}\:\sqrt{\mathrm{cos}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:{x}\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:{x}}\right] \\ $$$$=−\mathrm{2}\underset{\mathrm{1}} {\overset{\mathrm{0}} {\int}}\sqrt{{t}}{dt}=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{{t}}{dt}=\mathrm{2}\left[\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}/\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by liberty last updated on 17/Nov/20
![on interval −(π/2)≤x≤0 ⇒∣sin x∣ = −sin x sir ? it should be ∫_(−π/2) ^0 −sin x(√(cos x)) dx+∫_0 ^(π/2) sin x(√(cos x)) dx let cos x = u → { ((u=1)),((u=0)) :} ∫_0 ^1 (√u) du −∫_1 ^0 (√u) du = 2∫_0 ^1 (√u) du =[ (4/3)u^(3/2) ]_0 ^1 = (4/3).](Q122537.png)
$$\mathrm{on}\:\mathrm{interval}\:−\frac{\pi}{\mathrm{2}}\leqslant\mathrm{x}\leqslant\mathrm{0}\:\Rightarrow\mid\mathrm{sin}\:\mathrm{x}\mid\:=\:−\mathrm{sin}\:\mathrm{x}\:\mathrm{sir}\:? \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\underset{−\pi/\mathrm{2}} {\overset{\mathrm{0}} {\int}}−\mathrm{sin}\:\mathrm{x}\sqrt{\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}+\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{sin}\:\mathrm{x}\sqrt{\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{u}\:\rightarrow\begin{cases}{\mathrm{u}=\mathrm{1}}\\{\mathrm{u}=\mathrm{0}}\end{cases} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\mathrm{u}}\:\mathrm{du}\:−\underset{\mathrm{1}} {\overset{\mathrm{0}} {\int}}\sqrt{\mathrm{u}}\:\mathrm{du}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{u}}\:\mathrm{du} \\ $$$$=\left[\:\frac{\mathrm{4}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}/\mathrm{2}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{4}}{\mathrm{3}}. \\ $$
Commented by MJS_new last updated on 17/Nov/20
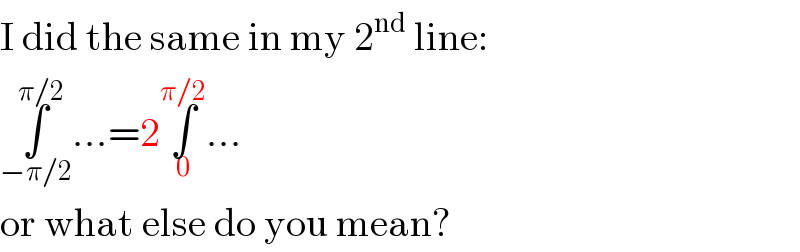
$$\mathrm{I}\:\mathrm{did}\:\mathrm{the}\:\mathrm{same}\:\mathrm{in}\:\mathrm{my}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{line}: \\ $$$$\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}...=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}... \\ $$$$\mathrm{or}\:\mathrm{what}\:\mathrm{else}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}? \\ $$
