
Question Number 46188 by rahul 19 last updated on 22/Oct/18
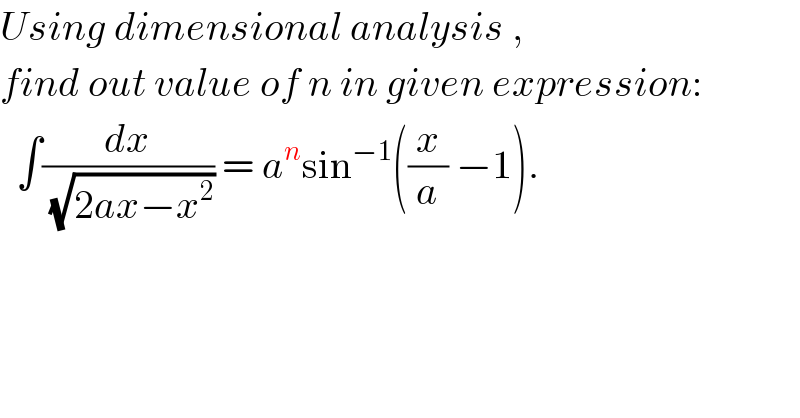
$${Using}\:{dimensional}\:{analysis}\:, \\ $$$${find}\:{out}\:{value}\:{of}\:{n}\:{in}\:{given}\:{expression}: \\ $$$$\:\:\int\frac{{dx}}{\sqrt{\mathrm{2}{ax}−{x}^{\mathrm{2}} }}\:=\:{a}^{{n}} \mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\:−\mathrm{1}\right). \\ $$
Commented by rahul 19 last updated on 22/Oct/18

Commented by rahul 19 last updated on 22/Oct/18
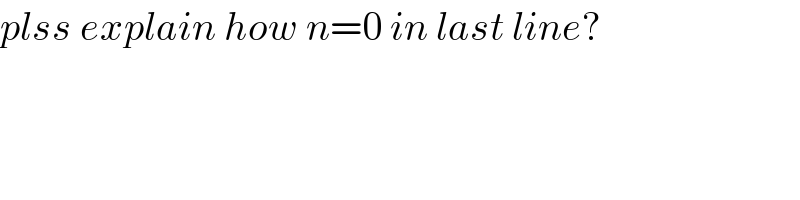
$${plss}\:{explain}\:{how}\:{n}=\mathrm{0}\:{in}\:{last}\:{line}? \\ $$
Commented by MrW3 last updated on 22/Oct/18
![dimension of left side is [L^0 ],i.e. no dimension dimension of right side is [L^n ], it should also be no dimension ⇒n=0](Q46193.png)
$${dimension}\:{of}\:{left}\:{side}\:{is}\:\left[{L}^{\mathrm{0}} \right],{i}.{e}.\:{no} \\ $$$${dimension} \\ $$$$ \\ $$$${dimension}\:{of}\:{right}\:{side}\:{is}\:\left[{L}^{{n}} \right],\:{it} \\ $$$${should}\:{also}\:{be}\:{no}\:{dimension} \\ $$$$ \\ $$$$\Rightarrow{n}=\mathrm{0} \\ $$
Commented by rahul 19 last updated on 22/Oct/18
Thanks sir ! ���� I got confused seeing zero in denominator!! Sir, do you have idea to how much extent we can apply dimensional analysis in integration? I'm seeing it for 1st time.
Commented by maxmathsup by imad last updated on 22/Oct/18
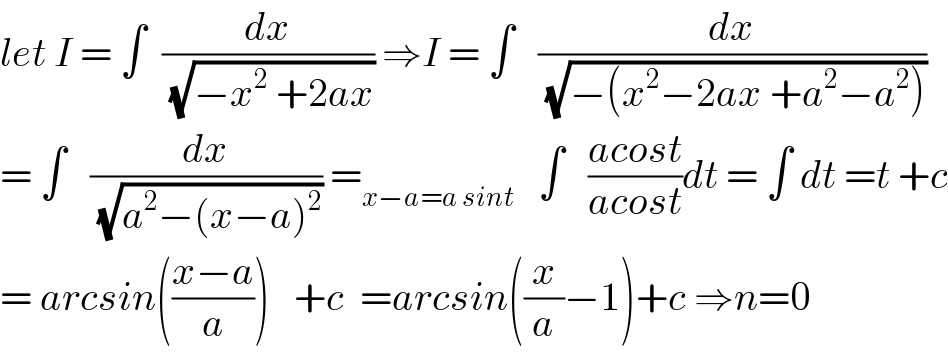
$${let}\:{I}\:=\:\int\:\:\frac{{dx}}{\sqrt{−{x}^{\mathrm{2}} \:+\mathrm{2}{ax}}}\:\Rightarrow{I}\:=\:\int\:\:\:\frac{{dx}}{\sqrt{−\left({x}^{\mathrm{2}} −\mathrm{2}{ax}\:+{a}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}} \\ $$$$=\:\int\:\:\:\frac{{dx}}{\sqrt{{a}^{\mathrm{2}} −\left({x}−{a}\right)^{\mathrm{2}} }}\:=_{{x}−{a}={a}\:{sint}} \:\:\:\int\:\:\:\frac{{acost}}{{acost}}{dt}\:=\:\int\:{dt}\:={t}\:+{c} \\ $$$$=\:{arcsin}\left(\frac{{x}−{a}}{{a}}\right)\:\:\:+{c}\:\:={arcsin}\left(\frac{{x}}{{a}}−\mathrm{1}\right)+{c}\:\Rightarrow{n}=\mathrm{0} \\ $$
