
Question Number 187606 by otchereabdullai last updated on 19/Feb/23
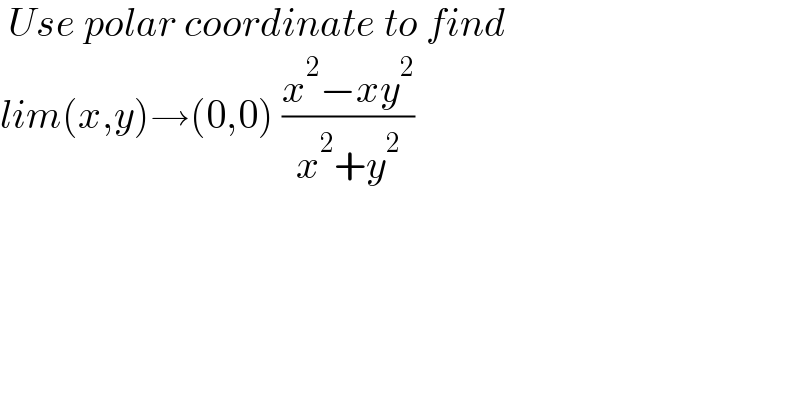
$$\:{Use}\:{polar}\:{coordinate}\:{to}\:{find}\: \\ $$$${lim}\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)\:\frac{{x}^{\mathrm{2}} −{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$
Answered by a.lgnaoui last updated on 19/Feb/23
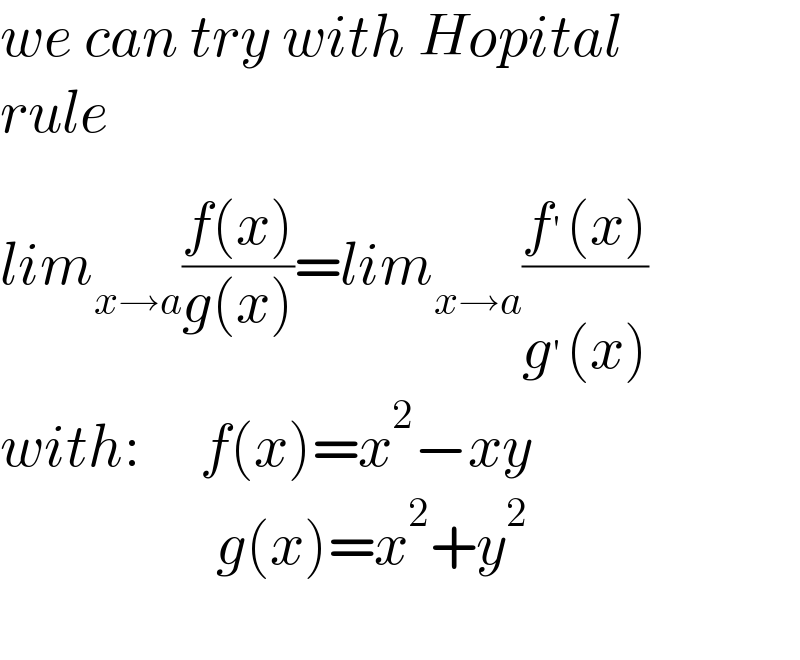
$${we}\:{can}\:{try}\:{with}\:{Hopital} \\ $$$${rule} \\ $$$${lim}_{{x}\rightarrow{a}} \frac{{f}\left({x}\right)}{{g}\left({x}\right)}={lim}_{{x}\rightarrow{a}} \frac{{f}^{'} \left({x}\right)}{{g}^{'} \left({x}\right)} \\ $$$${with}:\:\:\:\:\:{f}\left({x}\right)={x}^{\mathrm{2}} −{xy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{g}\left({x}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by mr W last updated on 20/Feb/23
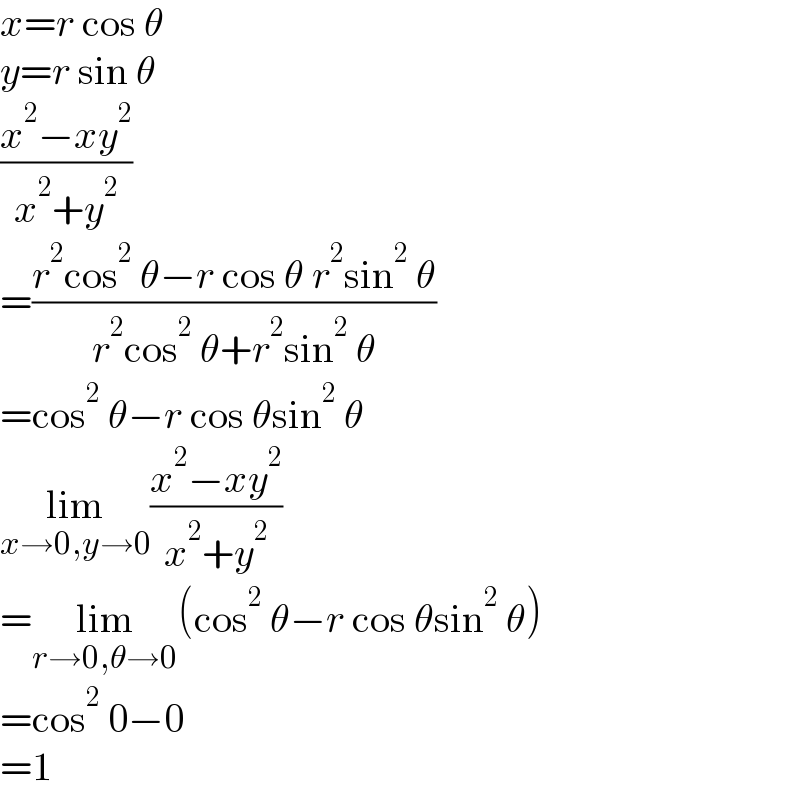
$${x}={r}\:\mathrm{cos}\:\theta \\ $$$${y}={r}\:\mathrm{sin}\:\theta \\ $$$$\frac{{x}^{\mathrm{2}} −{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$=\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta−{r}\:\mathrm{cos}\:\theta\:{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$=\mathrm{cos}^{\mathrm{2}} \:\theta−{r}\:\mathrm{cos}\:\theta\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\underset{{x}\rightarrow\mathrm{0},{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$=\underset{{r}\rightarrow\mathrm{0},\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cos}^{\mathrm{2}} \:\theta−{r}\:\mathrm{cos}\:\theta\mathrm{sin}^{\mathrm{2}} \:\theta\right) \\ $$$$=\mathrm{cos}^{\mathrm{2}} \:\mathrm{0}−\mathrm{0} \\ $$$$=\mathrm{1} \\ $$
Commented by otchereabdullai last updated on 20/Feb/23
$${Am}\:{much}\:{grateful}\:{prof}\:{W} \\ $$
