Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 69238 by ~ À ® @ 237 ~ last updated on 21/Sep/19

Use Residus Theorem to explicit f(a)=Σ_(n=1) ^∞ (((−1)^n sin(na))/n^3 )

$${Use}\:{Residus}\:{Theorem}\:{to}\:{explicit}\: \\ $$$${f}\left({a}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({na}\right)}{{n}^{\mathrm{3}} }\:\: \\ $$

Commented by mathmax by abdo last updated on 22/Sep/19

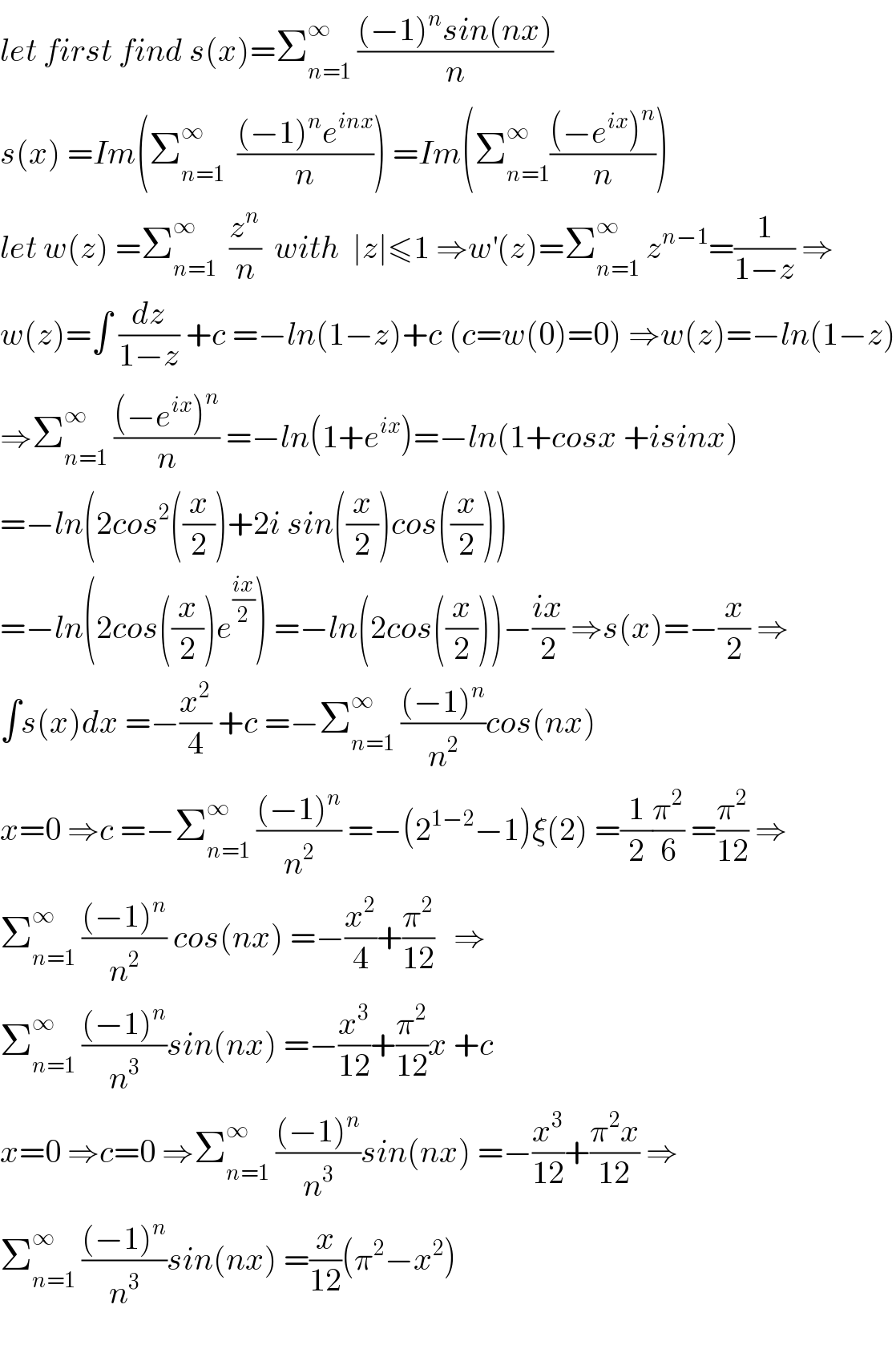
let first find s(x)=Σ_(n=1) ^∞ (((−1)^n sin(nx))/n) s(x) =Im(Σ_(n=1) ^∞ (((−1)^n e^(inx) )/n)) =Im(Σ_(n=1) ^∞ (((−e^(ix) )^n )/n)) let w(z) =Σ_(n=1) ^∞ (z^n /n) with ∣z∣≤1 ⇒w^′ (z)=Σ_(n=1) ^∞ z^(n−1) =(1/(1−z)) ⇒ w(z)=∫ (dz/(1−z)) +c =−ln(1−z)+c (c=w(0)=0) ⇒w(z)=−ln(1−z) ⇒Σ_(n=1) ^∞ (((−e^(ix) )^n )/n) =−ln(1+e^(ix) )=−ln(1+cosx +isinx) =−ln(2cos^2 ((x/2))+2i sin((x/2))cos((x/2))) =−ln(2cos((x/2))e^((ix)/2) ) =−ln(2cos((x/2)))−((ix)/2) ⇒s(x)=−(x/2) ⇒ ∫s(x)dx =−(x^2 /4) +c =−Σ_(n=1) ^∞ (((−1)^n )/n^2 )cos(nx) x=0 ⇒c =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−(2^(1−2) −1)ξ(2) =(1/2)(π^2 /6) =(π^2 /(12)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) cos(nx) =−(x^2 /4)+(π^2 /(12)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^3 )sin(nx) =−(x^3 /(12))+(π^2 /(12))x +c x=0 ⇒c=0 ⇒Σ_(n=1) ^∞ (((−1)^n )/n^3 )sin(nx) =−(x^3 /(12))+((π^2 x)/(12)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^3 )sin(nx) =(x/(12))(π^2 −x^2 )

$${let}\:{first}\:{find}\:{s}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({nx}\right)}{{n}} \\ $$$${s}\left({x}\right)\:={Im}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} {e}^{{inx}} }{{n}}\right)\:={Im}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−{e}^{{ix}} \right)^{{n}} }{{n}}\right) \\ $$$${let}\:{w}\left({z}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{z}^{{n}} }{{n}}\:\:{with}\:\:\mid{z}\mid\leqslant\mathrm{1}\:\Rightarrow{w}^{'} \left({z}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{z}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{z}}\:\Rightarrow \\ $$$${w}\left({z}\right)=\int\:\frac{{dz}}{\mathrm{1}−{z}}\:+{c}\:=−{ln}\left(\mathrm{1}−{z}\right)+{c}\:\left({c}={w}\left(\mathrm{0}\right)=\mathrm{0}\right)\:\Rightarrow{w}\left({z}\right)=−{ln}\left(\mathrm{1}−{z}\right) \\ $$$$\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−{e}^{{ix}} \right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{1}+{e}^{{ix}} \right)=−{ln}\left(\mathrm{1}+{cosx}\:+{isinx}\right) \\ $$$$=−{ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}{i}\:{sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$=−{ln}\left(\mathrm{2}{cos}\left(\frac{{x}}{\mathrm{2}}\right){e}^{\frac{{ix}}{\mathrm{2}}} \right)\:=−{ln}\left(\mathrm{2}{cos}\left(\frac{{x}}{\mathrm{2}}\right)\right)−\frac{{ix}}{\mathrm{2}}\:\Rightarrow{s}\left({x}\right)=−\frac{{x}}{\mathrm{2}}\:\Rightarrow \\ $$$$\int{s}\left({x}\right){dx}\:=−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:+{c}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }{cos}\left({nx}\right) \\ $$$${x}=\mathrm{0}\:\Rightarrow{c}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:{cos}\left({nx}\right)\:=−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} }{sin}\left({nx}\right)\:=−\frac{{x}^{\mathrm{3}} }{\mathrm{12}}+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}{x}\:+{c} \\ $$$${x}=\mathrm{0}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} }{sin}\left({nx}\right)\:=−\frac{{x}^{\mathrm{3}} }{\mathrm{12}}+\frac{\pi^{\mathrm{2}} {x}}{\mathrm{12}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} }{sin}\left({nx}\right)\:=\frac{{x}}{\mathrm{12}}\left(\pi^{\mathrm{2}} −{x}^{\mathrm{2}} \right) \\ $$$$ \\ $$

Answered by mind is power last updated on 22/Sep/19

We have limx→n ((π(x−n))/(sin(πx)))=(π/((sin(πx)_(x=n) ^′ ))=(−1)^n let f(z)=((πsin(za) )/(z^3 sin(nπ))) f has poles at z=n withe n∈Z^∗ of order 1 and in z=0 of order 3 let C_r squar of side r and center in 0 ⇒∫_C_r f(z)dz=Σ_Z_k 2iπ(Res (f∣z_k ) ′′Z_k ∈C_r ” and we have lim ∣zf(z)∣⇒0 By jordan lemma we get Lim r→+∞∫_C_r f(z)dz=0 Residus th ⇒Lim r→+∞ ∫_(cr) f(z)dz=Σ_(n∈^� IZ) 2iπRes(f(z)∣∣n) ⇒0=Res(f∣0)+Σ_(n∈IZ^∗ ) Res(f∣n) Res(f∣n)=lim z→n(((z−n)πsin(za))/(z^3 sin(πz)))=((πsin(na))/(n^3 πcos(nπ)))=(((−1)^n sin(na))/n^3 ) Res(f∣0) we use laurent serie ((sin(za))/z^3 ).(π/(sin(πz)))=(((za−(((za)^3 )/6)...))/z^3 ).(1/(πz−((π^3 z^3 )/6)..)) =(1/z^3 )(a−((z^2 a^3 )/6)...)(1+((π^2 z^2 )/6)...)=(a/z^3 )+(1/z)(((aπ^2 )/6)−(a^3 /6)).... Res(f∣0)=(a/6)(−a^2 +π^2 ) ⇒Σ_(∣n∣≥1) (((−1)^n sin(na))/n^3 )−(a/6)(a^2 −π^2 )=0 ⇒2Σ_(n=1) ^(+∞) (((−1)^n sin(na))/n^3 )=(a/6)(a^2 −π^2 ) ⇒Σ_(n=1) ^(+∞) (((−1)^n sin(na))/n^3 )=(a/(12))(a^2 −π^2 )

$${We}\:{have}\: \\ $$$${limx}\rightarrow{n}\:\frac{\pi\left({x}−{n}\right)}{{sin}\left(\pi{x}\right)}=\frac{\pi}{\left({sin}\left(\pi{x}\right)_{{x}={n}} ^{'} \right.}=\left(−\mathrm{1}\right)^{{n}} \\ $$$${let}\:{f}\left({z}\right)=\frac{\pi{sin}\left({za}\right)\:}{{z}^{\mathrm{3}} {sin}\left({n}\pi\right)} \\ $$$${f}\:{has}\:{poles}\:{at}\:{z}={n}\:{withe}\:{n}\in\mathbb{Z}^{\ast} {of}\:{order}\:\mathrm{1}\:{and}\:{in}\:{z}=\mathrm{0}\:{of}\:{order}\:\mathrm{3}\: \\ $$$${let}\:{C}_{{r}} \:{squar}\:{of}\:{side}\:{r}\:{and}\:{center}\:{in}\:\mathrm{0} \\ $$$$\Rightarrow\int_{{C}_{{r}} } {f}\left({z}\right){dz}=\sum_{{Z}_{{k}} } \mathrm{2}{i}\pi\left({Res}\:\left({f}\mid{z}_{{k}} \right)\:\:''{Z}_{{k}} \in{C}_{{r}} ''\right. \\ $$$${and}\:\:{we}\:{have}\:\:{lim}\:\mid{zf}\left({z}\right)\mid\Rightarrow\mathrm{0} \\ $$$${By}\:{jordan}\:{lemma}\:{we}\:{get}\:{Lim}\:{r}\rightarrow+\infty\int_{{C}_{{r}} } {f}\left({z}\right){dz}=\mathrm{0} \\ $$$${Residus}\:{th}\:\Rightarrow{Lim}\:{r}\rightarrow+\infty\:\int_{{cr}} {f}\left({z}\right){dz}=\underset{{n}\hat {\in}{IZ}} {\sum}\mathrm{2}{i}\pi{Res}\left({f}\left({z}\right)\mid\mid{n}\right) \\ $$$$\Rightarrow\mathrm{0}={Res}\left({f}\mid\mathrm{0}\right)+\sum_{{n}\in{IZ}^{\ast} } {Res}\left({f}\mid{n}\right) \\ $$$${Res}\left({f}\mid{n}\right)={lim}\:{z}\rightarrow{n}\frac{\left({z}−{n}\right)\pi{sin}\left({za}\right)}{{z}^{\mathrm{3}} {sin}\left(\pi{z}\right)}=\frac{\pi{sin}\left({na}\right)}{{n}^{\mathrm{3}} \pi{cos}\left({n}\pi\right)}=\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({na}\right)}{{n}^{\mathrm{3}} } \\ $$$${Res}\left({f}\mid\mathrm{0}\right)\:{we}\:{use}\:{laurent}\:{serie} \\ $$$$\frac{{sin}\left({za}\right)}{{z}^{\mathrm{3}} }.\frac{\pi}{{sin}\left(\pi{z}\right)}=\frac{\left({za}−\frac{\left({za}\right)^{\mathrm{3}} }{\mathrm{6}}...\right)}{{z}^{\mathrm{3}} }.\frac{\mathrm{1}}{\pi{z}−\frac{\pi^{\mathrm{3}} {z}^{\mathrm{3}} }{\mathrm{6}}..} \\ $$$$=\frac{\mathrm{1}}{{z}^{\mathrm{3}} }\left({a}−\frac{{z}^{\mathrm{2}} {a}^{\mathrm{3}} }{\mathrm{6}}...\right)\left(\mathrm{1}+\frac{\pi^{\mathrm{2}} {z}^{\mathrm{2}} }{\mathrm{6}}...\right)=\frac{{a}}{{z}^{\mathrm{3}} }+\frac{\mathrm{1}}{{z}}\left(\frac{{a}\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{{a}^{\mathrm{3}} }{\mathrm{6}}\right).... \\ $$$${Res}\left({f}\mid\mathrm{0}\right)=\frac{{a}}{\mathrm{6}}\left(−{a}^{\mathrm{2}} +\pi^{\mathrm{2}} \right) \\ $$$$\Rightarrow\sum_{\mid{n}\mid\geqslant\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({na}\right)}{{n}^{\mathrm{3}} }−\frac{{a}}{\mathrm{6}}\left({a}^{\mathrm{2}} −\pi^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\sum_{{n}=\mathrm{1}} ^{+\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({na}\right)}{{n}^{\mathrm{3}} }=\frac{{a}}{\mathrm{6}}\left({a}^{\mathrm{2}} −\pi^{\mathrm{2}} \right) \\ $$$$\Rightarrow\sum_{{n}=\mathrm{1}} ^{+\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({na}\right)}{{n}^{\mathrm{3}} }=\frac{{a}}{\mathrm{12}}\left({a}^{\mathrm{2}} −\pi^{\mathrm{2}} \right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com