
Question Number 201533 by Rodier97 last updated on 08/Dec/23
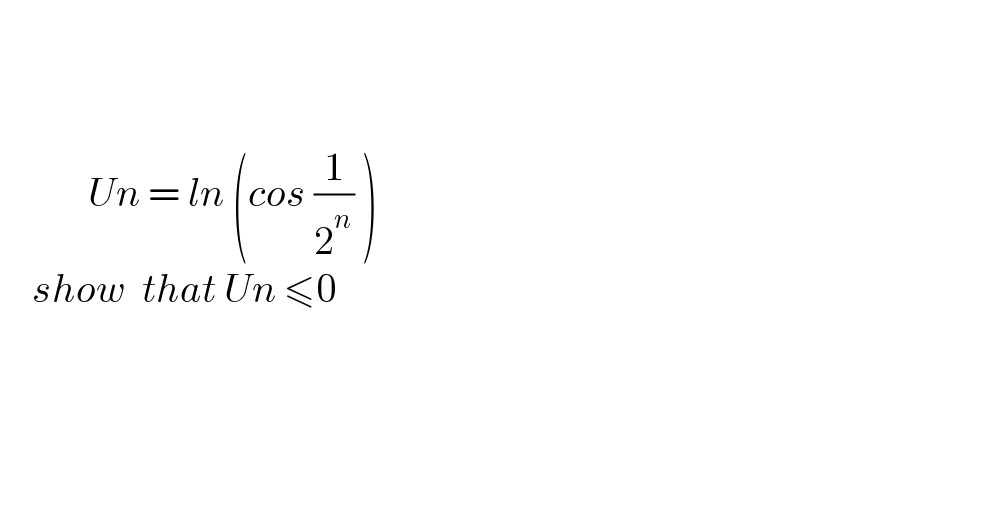
$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{Un}\:=\:{ln}\:\left({cos}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\right) \\ $$$$\:\:\:\:{show}\:\:{that}\:{Un}\:\leqslant\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by deleteduser1 last updated on 08/Dec/23
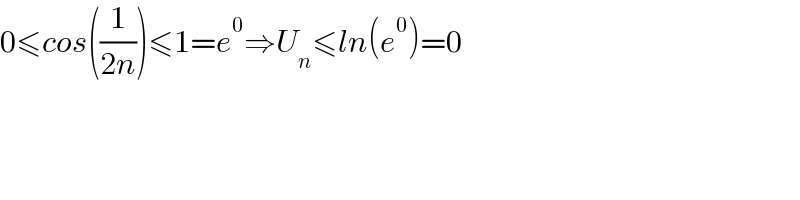
$$\mathrm{0}\leqslant{cos}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\leqslant\mathrm{1}={e}^{\mathrm{0}} \Rightarrow{U}_{{n}} \leqslant{ln}\left({e}^{\mathrm{0}} \right)=\mathrm{0} \\ $$
Answered by Mathspace last updated on 08/Dec/23
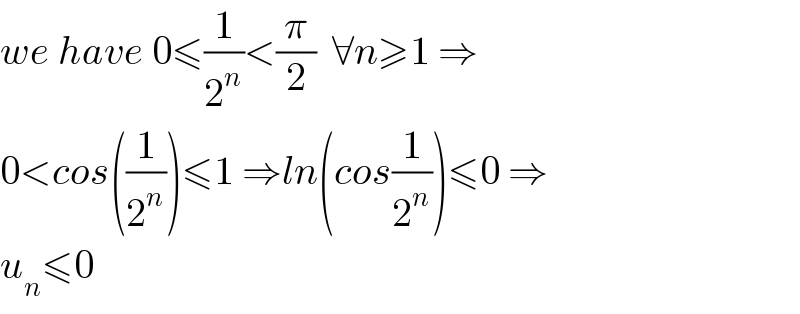
$${we}\:{have}\:\mathrm{0}\leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}} }<\frac{\pi}{\mathrm{2}}\:\:\forall{n}\geqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{0}<{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\leqslant\mathrm{1}\:\Rightarrow{ln}\left({cos}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\leqslant\mathrm{0}\:\Rightarrow \\ $$$${u}_{{n}} \leqslant\mathrm{0} \\ $$
