Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 213097 by issac last updated on 30/Oct/24

Uhhhh. can you guys solve Partial differantial equation ▽^2 𝛗=0 Cylinderical Laplacian case ▽^2 =(1/ρ)∙((∂ )/∂ρ)(ρ((∂ )/∂ρ))+((1/ρ))^2 (∂^2 /∂φ^2 )+((∂^2 )/∂z^2 ) Spherical Laplacian case ▽^2 =((1/r))^2 ((∂ )/∂r)(r^2 ((∂ )/∂r))+(1/(r^2 sin(θ)))∙((∂ )/∂θ)(sin(θ)((∂ )/∂θ))+(1/(r^2 sin^2 (θ)))∙(∂^2 /∂ϕ^2 )

$$\mathrm{Uhhhh}. \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{guys}\:\mathrm{solve}\:\mathrm{Partial}\:\mathrm{differantial}\:\mathrm{equation} \\ $$$$\bigtriangledown^{\mathrm{2}} \boldsymbol{\phi}=\mathrm{0} \\ $$$$\mathrm{Cylinderical}\:\mathrm{Laplacian}\:\mathrm{case} \\ $$$$\bigtriangledown^{\mathrm{2}} =\frac{\mathrm{1}}{\rho}\centerdot\frac{\partial\:\:}{\partial\rho}\left(\rho\frac{\partial\:\:}{\partial\rho}\right)+\left(\frac{\mathrm{1}}{\rho}\right)^{\mathrm{2}} \frac{\partial^{\mathrm{2}} \:}{\partial\phi^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \:\:}{\partial{z}^{\mathrm{2}} } \\ $$$$\mathrm{Spherical}\:\mathrm{Laplacian}\:\mathrm{case} \\ $$$$\bigtriangledown^{\mathrm{2}} =\left(\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} \frac{\partial\:\:}{\partial{r}}\left({r}^{\mathrm{2}} \frac{\partial\:\:}{\partial{r}}\right)+\frac{\mathrm{1}}{{r}^{\mathrm{2}} \mathrm{sin}\left(\theta\right)}\centerdot\frac{\partial\:\:}{\partial\theta}\left(\mathrm{sin}\left(\theta\right)\frac{\partial\:\:}{\partial\theta}\right)+\frac{\mathrm{1}}{{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\theta\right)}\centerdot\frac{\partial^{\mathrm{2}} \:}{\partial\varphi^{\mathrm{2}} } \\ $$

Answered by MrGaster last updated on 30/Oct/24

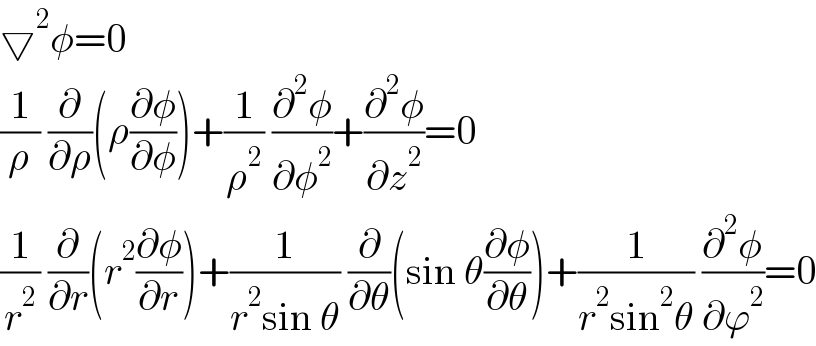
▽^2 φ=0 (1/ρ) (∂/∂ρ)(ρ(∂φ/∂φ))+(1/ρ^2 ) (∂^2 φ/∂φ^2 )+(∂^2 φ/∂z^2 )=0 (1/r^2 ) (∂/∂r)(r^2 (∂φ/∂r))+(1/(r^2 sin θ)) (∂/∂θ)(sin θ(∂φ/∂θ))+(1/(r^2 sin^2 θ)) (∂^2 φ/∂ϕ^2 )=0

$$\bigtriangledown^{\mathrm{2}} \phi=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\rho}\:\frac{\partial}{\partial\rho}\left(\rho\frac{\partial\phi}{\partial\phi}\right)+\frac{\mathrm{1}}{\rho^{\mathrm{2}} }\:\frac{\partial^{\mathrm{2}} \phi}{\partial\phi^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \phi}{\partial{z}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\:\frac{\partial}{\partial{r}}\left({r}^{\mathrm{2}} \frac{\partial\phi}{\partial{r}}\right)+\frac{\mathrm{1}}{{r}^{\mathrm{2}} \mathrm{sin}\:\theta}\:\frac{\partial}{\partial\theta}\left(\mathrm{sin}\:\theta\frac{\partial\phi}{\partial\theta}\right)+\frac{\mathrm{1}}{{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta}\:\frac{\partial^{\mathrm{2}} \phi}{\partial\varphi^{\mathrm{2}} }=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com