
Question Number 216807 by GDVilla last updated on 21/Feb/25

$$\mathrm{Uh}\:\mathrm{guys}\:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{formula} \\ $$$$\frac{{d}}{{t}} \\ $$$$\mathrm{or} \\ $$$$\mathrm{li}\underset{\Delta{t}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\Delta{d}}{\Delta{t}} \\ $$
Answered by MrGaster last updated on 21/Feb/25

$$\frac{\mathrm{d}}{{t}}\left(\mathrm{mean}\:\mathrm{velocity}\right) \\ $$$$\underset{\Delta{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\Delta{d}}{\Delta{t}}\left(\mathrm{instantaneous}\:\mathrm{velocity}\right) \\ $$$$\mathrm{These}\:\mathrm{two}\:\mathrm{formulas}\:\mathrm{are}\: \\ $$$$\mathrm{usedto}\:\mathrm{deal}\:\mathrm{with}\:\mathrm{differente} \\ $$$$\mathrm{sped}\:\mathrm{situations}. \\ $$
Commented by GDVilla last updated on 21/Feb/25
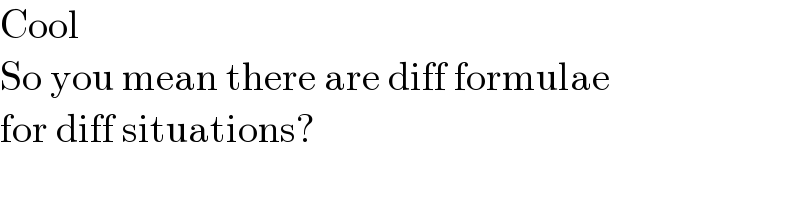
$$\mathrm{Cool} \\ $$$$\mathrm{So}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{there}\:\mathrm{are}\:\mathrm{diff}\:\mathrm{formulae} \\ $$$$\mathrm{for}\:\mathrm{diff}\:\mathrm{situations}? \\ $$
