
Question Number 159403 by LEKOUMA last updated on 16/Nov/21
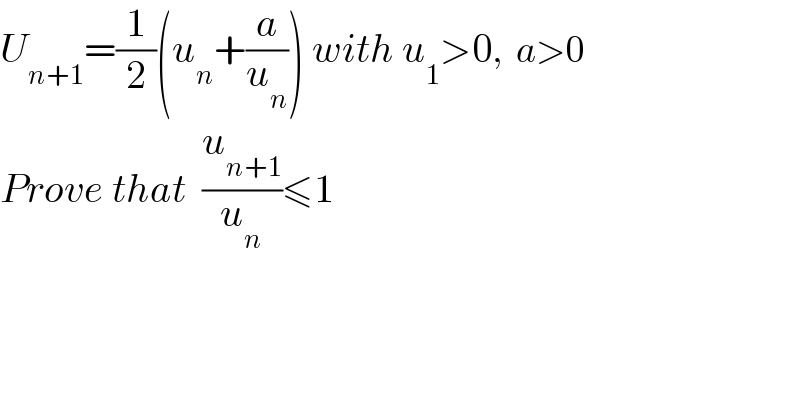
$${U}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}} +\frac{{a}}{{u}_{{n}} }\right)\:{with}\:{u}_{\mathrm{1}} >\mathrm{0},\:\:{a}>\mathrm{0} \\ $$$${Prove}\:{that}\:\:\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }\leqslant\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 18/Nov/21

$$\mathrm{i}\:\mathrm{think}\:\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\:\geqslant\mathrm{1}\:... \\ $$
