
Question Number 19654 by Tinkutara last updated on 13/Aug/17

$$\mathrm{Two}\:\mathrm{swimmers}\:\mathrm{leave}\:\mathrm{point}\:{A}\:\mathrm{on}\:\mathrm{one} \\ $$$$\mathrm{bank}\:\mathrm{of}\:\mathrm{the}\:\mathrm{river}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{point}\:{B}\:\mathrm{lying} \\ $$$$\mathrm{right}\:\mathrm{across}\:\mathrm{the}\:\mathrm{other}\:\mathrm{bank}.\:\mathrm{One}\:\mathrm{of} \\ $$$$\mathrm{them}\:\mathrm{crosses}\:\mathrm{the}\:\mathrm{river}\:\mathrm{along}\:\mathrm{the}\:\mathrm{straight} \\ $$$$\mathrm{line}\:{AB}\:\mathrm{while}\:\mathrm{the}\:\mathrm{other}\:\mathrm{swims}\:\mathrm{at}\:\mathrm{right} \\ $$$$\mathrm{angle}\:\mathrm{to}\:\mathrm{the}\:\mathrm{stream}\:\mathrm{and}\:\mathrm{then}\:\mathrm{walks}\:\mathrm{the} \\ $$$$\mathrm{distance}\:\mathrm{that}\:\mathrm{he}\:\mathrm{has}\:\mathrm{been}\:\mathrm{carried}\:\mathrm{away} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{stream}\:\mathrm{to}\:\mathrm{get}\:\mathrm{to}\:\mathrm{point}\:{B}.\:\mathrm{What} \\ $$$$\mathrm{was}\:\mathrm{the}\:\mathrm{velocity}\:{v}\:\mathrm{of}\:\mathrm{his}\:\mathrm{walking}\:\mathrm{if}\:\mathrm{both} \\ $$$$\mathrm{swimmers}\:\mathrm{reached}\:\mathrm{the}\:\mathrm{destination} \\ $$$$\mathrm{simultaneously}?\:\left(\mathrm{The}\:\mathrm{stream}\:\mathrm{velocity}\right. \\ $$$${v}_{\mathrm{0}} \:=\:\mathrm{2}\:\mathrm{km}/\mathrm{h}\:\mathrm{and}\:\mathrm{the}\:\mathrm{velocity}\:{v}'\:\mathrm{of}\:\mathrm{each} \\ $$$$\mathrm{swimmer}\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{still}\:\mathrm{water}\:\mathrm{is} \\ $$$$\left.\mathrm{2}.\mathrm{5}\:\mathrm{km}/\mathrm{h}\right). \\ $$
Commented by ajfour last updated on 14/Aug/17
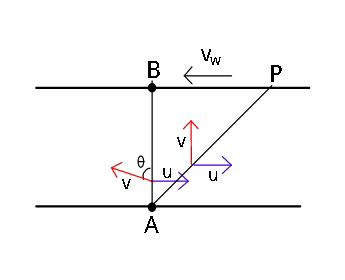
Commented by ajfour last updated on 14/Aug/17
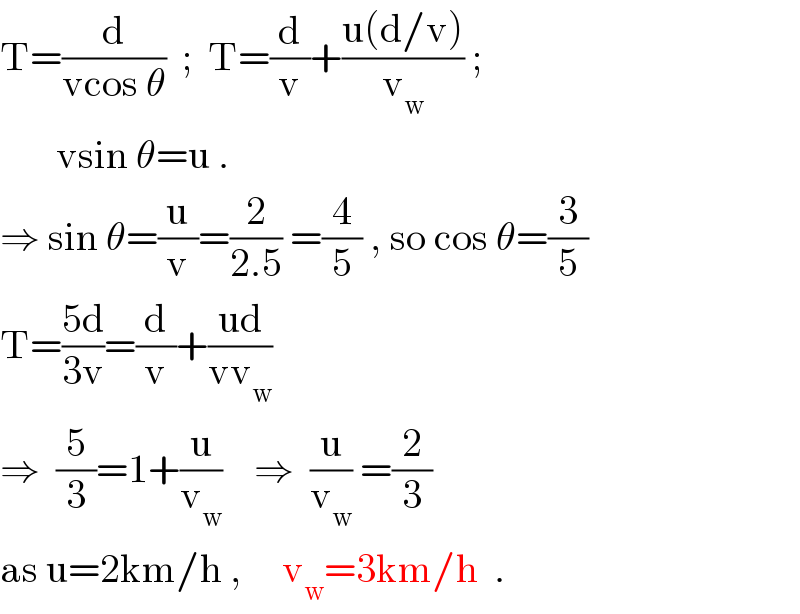
$$\mathrm{T}=\frac{\mathrm{d}}{\mathrm{vcos}\:\theta}\:\:;\:\:\mathrm{T}=\frac{\mathrm{d}}{\mathrm{v}}+\frac{\mathrm{u}\left(\mathrm{d}/\mathrm{v}\right)}{\mathrm{v}_{\mathrm{w}} }\:; \\ $$$$\:\:\:\:\:\:\:\mathrm{vsin}\:\theta=\mathrm{u}\:. \\ $$$$\Rightarrow\:\mathrm{sin}\:\theta=\frac{\mathrm{u}}{\mathrm{v}}=\frac{\mathrm{2}}{\mathrm{2}.\mathrm{5}}\:=\frac{\mathrm{4}}{\mathrm{5}}\:,\:\mathrm{so}\:\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{T}=\frac{\mathrm{5d}}{\mathrm{3v}}=\frac{\mathrm{d}}{\mathrm{v}}+\frac{\mathrm{ud}}{\mathrm{vv}_{\mathrm{w}} } \\ $$$$\Rightarrow\:\:\frac{\mathrm{5}}{\mathrm{3}}=\mathrm{1}+\frac{\mathrm{u}}{\mathrm{v}_{\mathrm{w}} }\:\:\:\:\Rightarrow\:\:\frac{\mathrm{u}}{\mathrm{v}_{\mathrm{w}} }\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{as}\:\mathrm{u}=\mathrm{2km}/\mathrm{h}\:,\:\:\:\:\:\mathrm{v}_{\mathrm{w}} =\mathrm{3km}/\mathrm{h}\:\:. \\ $$
Commented by Tinkutara last updated on 14/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
