Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 59505 by pete last updated on 11/May/19

Two particles P and Q move towards each other along a straight line MN, 51 meters long. P starts fromM with velocity 5 ms^(−1) and constant acceleration of 1 ms^(−2) . Q starts from N at the same time with velocity 6 ms^(−1) and at a constant acceleration of 3 ms^(−2) . Find the time when the: (a) particles are 30 metres apart; (b) particles meet; (c) velocity of P is (3/4) os the velocity of Q.

$$\mathrm{Two}\:\mathrm{particles}\:\mathrm{P}\:\mathrm{and}\:\mathrm{Q}\:\mathrm{move}\:\mathrm{towards}\:\mathrm{each} \\ $$$$\mathrm{other}\:\mathrm{along}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:{MN},\:\mathrm{51}\:\mathrm{meters} \\ $$$$\mathrm{long}.\:\mathrm{P}\:\mathrm{starts}\:\mathrm{from}{M}\:\mathrm{with}\:\mathrm{velocity}\:\mathrm{5}\:\mathrm{ms}^{−\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{constant}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{1}\:\mathrm{ms}^{−\mathrm{2}} .\:\mathrm{Q}\:\mathrm{starts} \\ $$$$\mathrm{from}\:\mathrm{N}\:\mathrm{at}\:\mathrm{the}\:\mathrm{same}\:\mathrm{time}\:\mathrm{with}\:\mathrm{velocity}\:\mathrm{6}\:\mathrm{ms}^{−\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{at}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{3}\:\mathrm{ms}^{−\mathrm{2}} . \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{time}\:\mathrm{when}\:\mathrm{the}: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{particles}\:\mathrm{are}\:\mathrm{30}\:\mathrm{metres}\:\mathrm{apart}; \\ $$$$\left(\mathrm{b}\right)\:\mathrm{particles}\:\mathrm{meet}; \\ $$$$\left(\mathrm{c}\right)\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{P}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{os}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{Q}. \\ $$

Answered by MJS last updated on 11/May/19

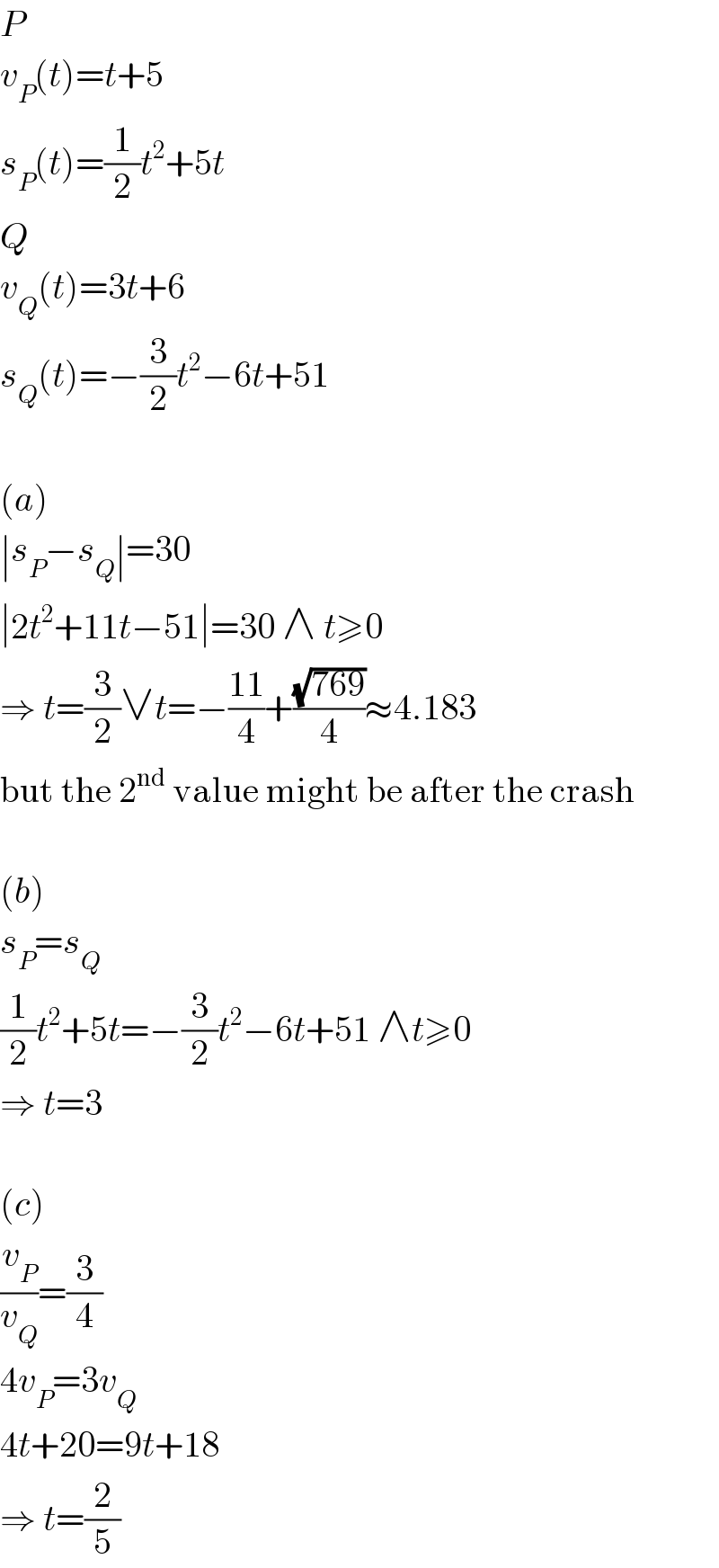
P v_P (t)=t+5 s_P (t)=(1/2)t^2 +5t Q v_Q (t)=3t+6 s_Q (t)=−(3/2)t^2 −6t+51 (a) ∣s_P −s_Q ∣=30 ∣2t^2 +11t−51∣=30 ∧ t≥0 ⇒ t=(3/2)∨t=−((11)/4)+((√(769))/4)≈4.183 but the 2^(nd) value might be after the crash (b) s_P =s_Q (1/2)t^2 +5t=−(3/2)t^2 −6t+51 ∧t≥0 ⇒ t=3 (c) (v_P /v_Q )=(3/4) 4v_P =3v_Q 4t+20=9t+18 ⇒ t=(2/5)

$${P} \\ $$$${v}_{{P}} \left({t}\right)={t}+\mathrm{5} \\ $$$${s}_{{P}} \left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{5}{t} \\ $$$${Q} \\ $$$${v}_{{Q}} \left({t}\right)=\mathrm{3}{t}+\mathrm{6} \\ $$$${s}_{{Q}} \left({t}\right)=−\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{51} \\ $$$$ \\ $$$$\left({a}\right) \\ $$$$\mid{s}_{{P}} −{s}_{{Q}} \mid=\mathrm{30} \\ $$$$\mid\mathrm{2}{t}^{\mathrm{2}} +\mathrm{11}{t}−\mathrm{51}\mid=\mathrm{30}\:\wedge\:{t}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{t}=\frac{\mathrm{3}}{\mathrm{2}}\vee{t}=−\frac{\mathrm{11}}{\mathrm{4}}+\frac{\sqrt{\mathrm{769}}}{\mathrm{4}}\approx\mathrm{4}.\mathrm{183} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{value}\:\mathrm{might}\:\mathrm{be}\:\mathrm{after}\:\mathrm{the}\:\mathrm{crash} \\ $$$$ \\ $$$$\left({b}\right) \\ $$$${s}_{{P}} ={s}_{{Q}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{5}{t}=−\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{51}\:\wedge{t}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{t}=\mathrm{3} \\ $$$$ \\ $$$$\left({c}\right) \\ $$$$\frac{{v}_{{P}} }{{v}_{{Q}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{4}{v}_{{P}} =\mathrm{3}{v}_{{Q}} \\ $$$$\mathrm{4}{t}+\mathrm{20}=\mathrm{9}{t}+\mathrm{18} \\ $$$$\Rightarrow\:{t}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$

Commented by pete last updated on 11/May/19

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 11/May/19

velocity of P w.r.t. Q be v displacement of P w.r.t. Q be s v=11+4t s=11t+2t^2 2t^2 +11t−21=0 ⇒ t=((−11+(√(121+169)))/4) = ((−11+(√(290)))/4) s ≈ 1.5s 2t^2 +11t−51=0 ⇒ t=((−11+(√(121+408)))/4) = 3s 5+t=(3/4)(6+3t) ⇒ 20+4t=18+9t t=(2/5)s .

$$\mathrm{velocity}\:\mathrm{of}\:\mathrm{P}\:\mathrm{w}.\mathrm{r}.\mathrm{t}.\:\mathrm{Q}\:\mathrm{be}\:\mathrm{v} \\ $$$$\mathrm{displacement}\:\mathrm{of}\:\mathrm{P}\:\mathrm{w}.\mathrm{r}.\mathrm{t}.\:\mathrm{Q}\:\mathrm{be}\:\mathrm{s} \\ $$$$\:\:\:\:\:\mathrm{v}=\mathrm{11}+\mathrm{4t} \\ $$$$\:\:\:\:\:\mathrm{s}=\mathrm{11t}+\mathrm{2t}^{\mathrm{2}} \\ $$$$\mathrm{2t}^{\mathrm{2}} +\mathrm{11t}−\mathrm{21}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{t}=\frac{−\mathrm{11}+\sqrt{\mathrm{121}+\mathrm{169}}}{\mathrm{4}}\:=\:\frac{−\mathrm{11}+\sqrt{\mathrm{290}}}{\mathrm{4}}\:\mathrm{s} \\ $$$$\:\:\approx\:\mathrm{1}.\mathrm{5s} \\ $$$$\mathrm{2t}^{\mathrm{2}} +\mathrm{11t}−\mathrm{51}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{t}=\frac{−\mathrm{11}+\sqrt{\mathrm{121}+\mathrm{408}}}{\mathrm{4}}\:=\:\mathrm{3s} \\ $$$$\mathrm{5}+\mathrm{t}=\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{6}+\mathrm{3t}\right) \\ $$$$\Rightarrow\:\:\:\:\mathrm{20}+\mathrm{4t}=\mathrm{18}+\mathrm{9t} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{t}=\frac{\mathrm{2}}{\mathrm{5}}\mathrm{s}\:. \\ $$

Commented by pete last updated on 11/May/19

Thank you very much sir

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com