
Question Number 217064 by ArshadS last updated on 28/Feb/25
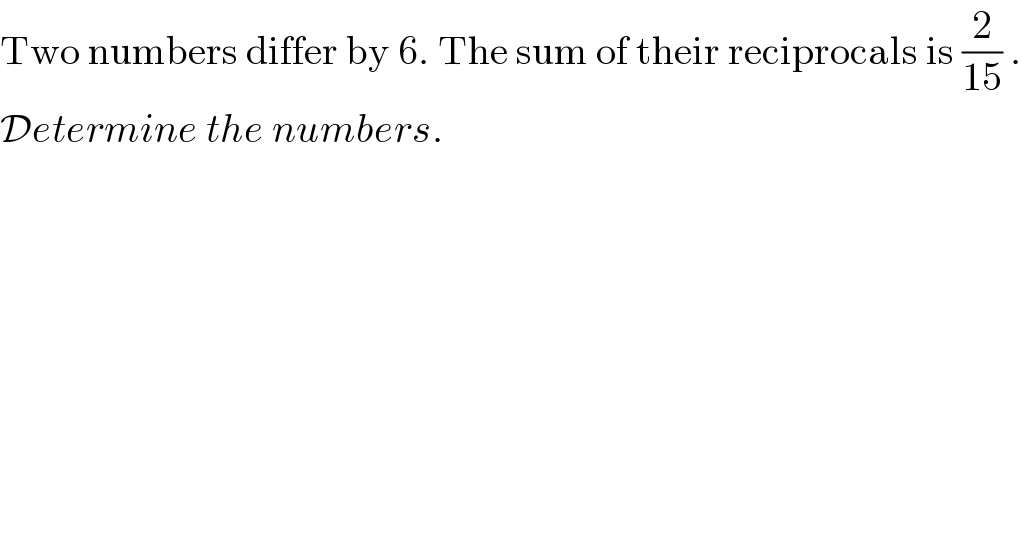
$$\mathrm{Two}\:\mathrm{numbers}\:\mathrm{differ}\:\mathrm{by}\:\mathrm{6}.\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{reciprocals}\:\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{15}}\:. \\ $$$$\mathcal{D}{etermine}\:{the}\:{numbers}. \\ $$
Answered by A5T last updated on 28/Feb/25
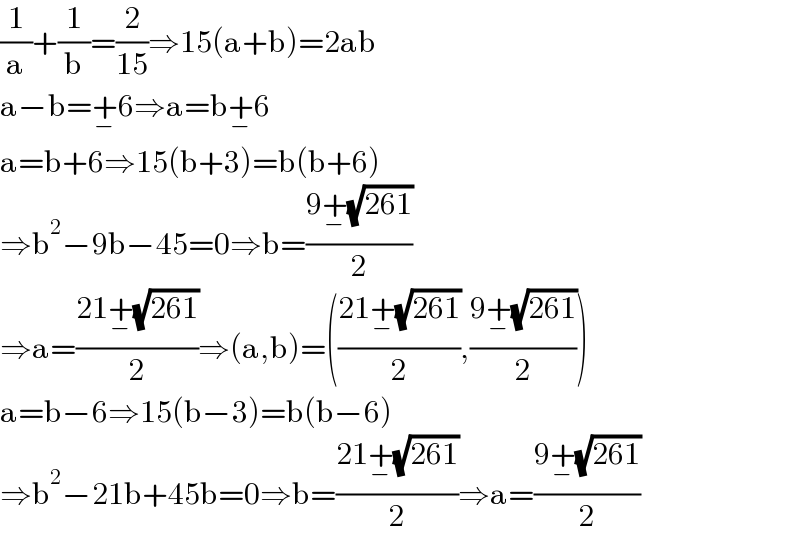
$$\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{2}}{\mathrm{15}}\Rightarrow\mathrm{15}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{2ab} \\ $$$$\mathrm{a}−\mathrm{b}=\underset{−} {+}\mathrm{6}\Rightarrow\mathrm{a}=\mathrm{b}\underset{−} {+}\mathrm{6} \\ $$$$\mathrm{a}=\mathrm{b}+\mathrm{6}\Rightarrow\mathrm{15}\left(\mathrm{b}+\mathrm{3}\right)=\mathrm{b}\left(\mathrm{b}+\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{9b}−\mathrm{45}=\mathrm{0}\Rightarrow\mathrm{b}=\frac{\mathrm{9}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{21}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\frac{\mathrm{21}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}},\frac{\mathrm{9}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}}\right) \\ $$$$\mathrm{a}=\mathrm{b}−\mathrm{6}\Rightarrow\mathrm{15}\left(\mathrm{b}−\mathrm{3}\right)=\mathrm{b}\left(\mathrm{b}−\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} −\mathrm{21b}+\mathrm{45b}=\mathrm{0}\Rightarrow\mathrm{b}=\frac{\mathrm{21}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}}\Rightarrow\mathrm{a}=\frac{\mathrm{9}\underset{−} {+}\sqrt{\mathrm{261}}}{\mathrm{2}} \\ $$
Commented by ArshadS last updated on 28/Feb/25

$$\mathrm{Thanks}\:\mathrm{sir}! \\ $$
