
Question Number 211127 by behi834171 last updated on 28/Aug/24

$$ \\ $$Two circles are assumed that have the same center. How many circles are there that are tangent to both circles and pass through the assumed point?
Commented by mr W last updated on 29/Aug/24
$${what}\:{do}\:{you}\:{mean}\:{with}\:``{the}\:{assumed} \\ $$$${point}''?\:{where}\:{does}\:{this}\:{point}\:{lie}? \\ $$
Commented by mr W last updated on 29/Aug/24
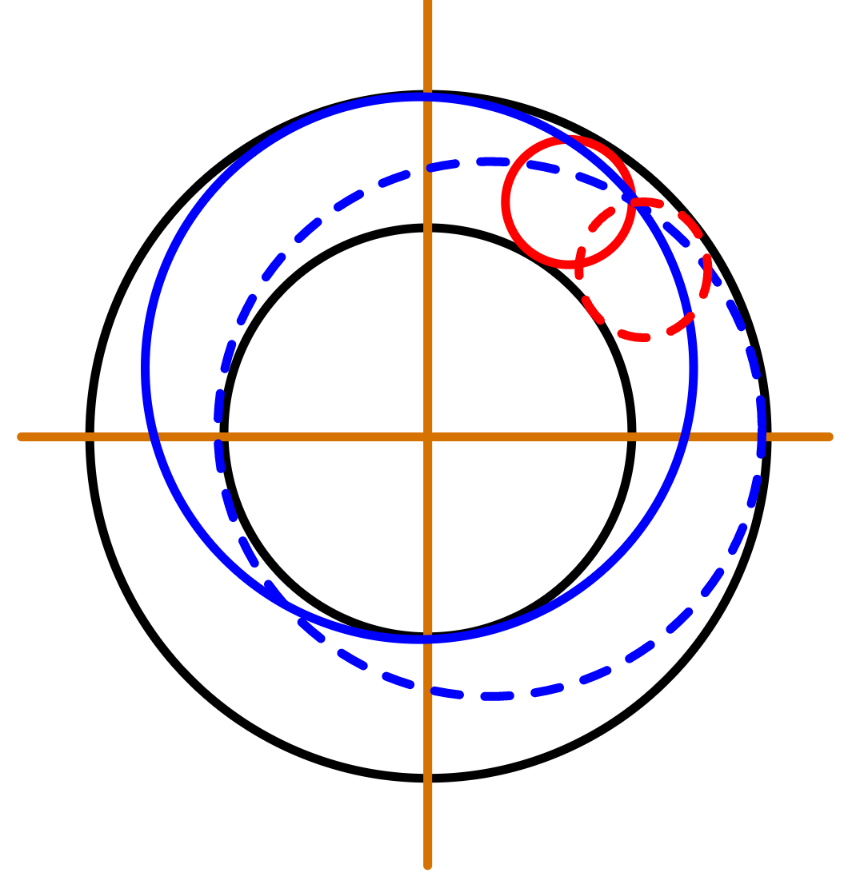
$${if}\:{this}\:{point}\:{lies}\:{in}\:{the}\:{ring}\:{area}, \\ $$$${then}\:{there}\:{are}\:\mathrm{4}\:{circles}\:{which} \\ $$$${tangent}\:{both}\:{circles}\:{and}\:{pass}\:{through} \\ $$$${this}\:{point}. \\ $$
Commented by mr W last updated on 29/Aug/24
Commented by behi834171 last updated on 29/Aug/24

$$ \\ $$Thank you for your attention,sir mr.W. The point can be anywhere: inside the any one of two concentric circles,or,on the side of the outer circle,or outside both circles.
Commented by mr W last updated on 29/Aug/24

$${only}\:{when}\:{the}\:{point}\:{lies}\:{between} \\ $$$${the}\:{two}\:{concentric}\:{circles},\:{as}\:{shown} \\ $$$${in}\:{the}\:{example}\:{above},\:{there}\:{exist} \\ $$$${circles}\:{which}\:{tangent}\:{the}\:{both}\: \\ $$$${circles}. \\ $$
Commented by behi834171 last updated on 29/Aug/24

$${Thank}\:{you}\:{so}\:{much}\:{dear}\:{master}. \\ $$$${if}\:{the}\:{radii}\:{of}\:{cocentric}\:{circles}\:\:{are}\:{given}, \\ $$$${is}\:{it}\:{possible}\:{to}\:{find}\:{the}\:{radii}\:{of}\: \\ $$$${tangent}\:{circles}? \\ $$
Commented by mr W last updated on 29/Aug/24

$${yes}.\:{say}\:{the}\:{radius}\:{of}\:{big}\:{circle}\:{is}\:{R} \\ $$$${and}\:{the}\:{radius}\:{of}\:{small}\:{circle}\:{is}\:{r}, \\ $$$${then}\:{the}\:{radius}\:{of}\:{the}\:{circles}\:{which} \\ $$$${tangent}\:{these}\:{two}\:{circles}\:{is} \\ $$$${r}_{\mathrm{1}} =\frac{{R}−{r}}{\mathrm{2}}\:\left({the}\:{red}\:{ones}\right)\:{or} \\ $$$${r}_{\mathrm{2}} =\frac{{R}+{r}}{\mathrm{2}}\:\left({the}\:{blues}\:{ones}\right) \\ $$
